题目内容

△ABC中，M是BC边的中点，则向量
AM
等于（　　）
A、
AB
-
AC
B、
1
2
（
AB
-
AC
）
C、
AB
+
AC
D、
1
2
（
AB
+
AC
）
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：根据向量加法的平行四边形法则，以及平行四边形的性质可得
解答： 解：根据平行四边形法则以及平行四边形的性质，
有
AM
=
1
2
(
AB
+
AC
)．
故选：D．
点评：本题考查向量加法的平行四边形法则，以及平行四边形的性质，
练习册系列答案
相关题目
在运动场上，两定点A和B，AB=6，运动员C可以走动，在此变动的平面三角形ABC中，该运动员走动始终满足AC+BC=8，当△ABC面积为7时，则运动员C看A、B两点的视角是
 
．
如图所示椭圆中，P为椭圆上一点，F为其一个焦点，PF为直径的圆与长轴为直径的圆的关系为
 
．
点A（2，3）到直线3x-4y+2=0的距离为
 
．
在集合{1，2，3，4，5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
a
=（a，b），从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形，记所有作成的平行四边形的个数为t，在区间（1，
t
3
）和（2，4）内分别各取一个数，记为m和n，则方程
x2
m2
+
y2
n2
=1表示焦点在x轴上的椭圆的概率P为
 
．
在棱长为3，各面都为等边三角形的正四面体内任取一点P，由点P向各面引垂线，垂线段的长度分别为d1，d2，d3，d4，则d1+d2+d3+d4的值为（　　）
A、
2
B、
3
C、2
D、
6
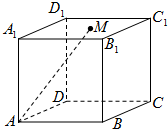
如图，ABCD-A1B1C1D1是正方体，在底面A1B1C1D1上任取一点M，则∠MAA1≤
π
6
的概率P=（　　）
A、
π
15
B、
π
12
C、
π
9
D、
π
6
定义在R上的可导函数f（x），若x≠1时，（x-1）f′（x）＜0恒成立（其中f′（x）是f（x）的导函数），则下列各项中一定正确的是（　　）
A、f（0）+f（2）＞2 f（1）
B、f（0）+f（2）=2f（1）
C、f（0）+f（2）＜2 f（1）
D、不能确定
若tan（2π+α）=
3
4
，则tan（α+
π
4
）=（　　）
A、
1
7
B、7
C、-
1
7
D、-7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网