题目内容
已知0<a<1,求证:
+
≥9.
| 1 |
| a |
| 4 |
| 1-a |
考点:不等式的证明
专题:证明题
分析:0<a<1⇒1-a>0,利用分析法,要证明
+
≥9,只需证明(3a-1)2≥0,该式成立,从而使结论得证.
| 1 |
| a |
| 4 |
| 1-a |
解答:
证明:由于0<a<1,∴1-a>0.
要证明
+
≥9,
只需证明1-a+4a≥9a-9a2,即9a2-6a+1≥0.
只需证明(3a-1)2≥0,
∵(3a-1)2≥0,显然成立,
∴原不等式成立.
要证明
| 1 |
| a |
| 4 |
| 1-a |
只需证明1-a+4a≥9a-9a2,即9a2-6a+1≥0.
只需证明(3a-1)2≥0,
∵(3a-1)2≥0,显然成立,
∴原不等式成立.
点评:本题考查分析法证明不等式,掌握分析法证题的逻辑关系与语言表达是关键,考查推理论证能力,属于中档题.

练习册系列答案
相关题目
执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( )


| A、[-6,-2] |
| B、[-5,-1] |
| C、[-4,5] |
| D、[-3,6] |
已知向量
=(1,
),
=(3,m),若向量
,
的夹角为
,则实数m=( )
| a |
| 3 |
| b |
| a |
| b |
| π |
| 6 |
A、2
| ||
B、
| ||
| C、0 | ||
D、-
|
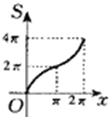
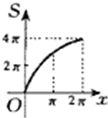
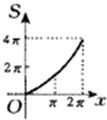
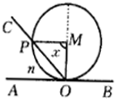 如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )
如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )