题目内容
已知等差数列{an}的前n项和Sn,a5=5,S5=15,则数列{
}的前2014项的和为 .
| 1 |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:联立方程组求得d及a1,
=
=
-
,利用裂项求和即可得出结论.
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:设等差数列的公差为d
由题意可得,
解方程可得,d=1,a1=1
由等差数列的通项公式可得,an=a1+(n-1)d=1+(n-1)×1=n
∴
=
=
-
∴S2014=1-
+
-
+…+
-
=1-
=
.
故答案为:
.
由题意可得,
|
由等差数列的通项公式可得,an=a1+(n-1)d=1+(n-1)×1=n
∴
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴S2014=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| 2014 |
| 2015 |
故答案为:
| 2014 |
| 2015 |
点评:本题考查学生数列的基本运算能力及裂项法求数列和,考查方程组思想的运用能力,属中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知向量
=(1,
),
=(3,m),若向量
,
的夹角为
,则实数m=( )
| a |
| 3 |
| b |
| a |
| b |
| π |
| 6 |
A、2
| ||
B、
| ||
| C、0 | ||
D、-
|
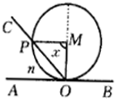 如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )
如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )A、 |
B、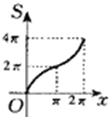 |
C、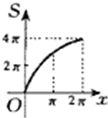 |
D、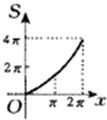 |
设复数z1=1-ai,z2=(2+i)2(i为虚数单位),若复数
在复平面内对应的点在直线5x-5y+3=0上,则a=( )
| z1 |
| z2 |
| A、6 | B、-6 | C、-22 | D、22 |
 如图,在△ABC中,sin
如图,在△ABC中,sin