题目内容
在平面直角坐标平面上,
=(1,4),
=(-3,1),且
与
在直线l的方向向量上的投影的长度相等,则直线l的斜率为( )
| OA |
| OB |
| OA |
| OB |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设直线l的一个方向向量为
=(1,k),由投影的意义可得
=
,再利用数量积运算解出即可.
| v |
|
| ||||
|
|
|
| ||||
|
|
解答:
解:设直线l的一个方向向量为
=(1,k),
由题意可得
=
,
∴|1+4k|=|-3+k|,
解得k=
或-
.
故选:C.
| v |
由题意可得
|
| ||||
|
|
|
| ||||
|
|
∴|1+4k|=|-3+k|,
解得k=
| 2 |
| 5 |
| 4 |
| 3 |
故选:C.
点评:本题考查了投影的意义、数量积运算,属于基础题.

练习册系列答案
相关题目
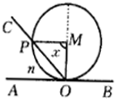 如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )
如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )A、 |
B、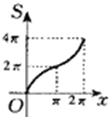 |
C、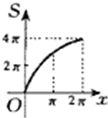 |
D、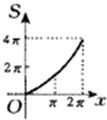 |
已知函数f(x)在定义域R上的值不全为零,若函数f(x+1)的图象关于(1,0)对称,函数f(x+3)的图象关于直线x=1对称,则下列式子中错误的是( )
| A、f(-x)=f(x) |
| B、f(x-2)=f(x+6) |
| C、f(-2+x)+f(-2-x)=0 |
| D、f(3+x)+f(3-x)=0 |
设i是虚数单位,
表示复数z的共轭复数.若z=1+i,则
+i•
=( )
. |
| z |
| z |
| i |
. |
| z |
| A、-2 | B、-2i | C、2 | D、2i |
 如图,在△ABC中,sin
如图,在△ABC中,sin