题目内容
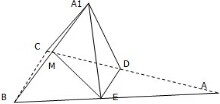已知在△ABC中，D，E分别为AC，AB的中点，沿DE将三角形ADE折起，使A到达A′的位置，若M是A′B的中点，求证：ME∥平面A′CD．考点：直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：取A′C的中点G，连结EM、MG、GD，证明四边形DEMG是平行四边形，可得ME∥DG，利用线面平行的判定定理证明ME∥平面A′CD．
解答：
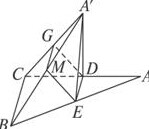证明：如图，取A′C的中点G，连结EM、MG、GD．
∵M、G分别是A′B、A′C的中点，
∴MG∥BC且MG=
BC．同理，DE∥BC且DE=
BC．
∴MG∥DE，MG=DE．
∴四边形DEMG是平行四边形．
∴ME∥DG．
又ME?面A′CD，DG?平面A′CD，
∴ME∥平面A′CD．
证明：如图，取A′C的中点G，连结EM、MG、GD．∵M、G分别是A′B、A′C的中点，
∴MG∥BC且MG=
| 1 |
| 2 |
| 1 |
| 2 |
∴MG∥DE，MG=DE．
∴四边形DEMG是平行四边形．
∴ME∥DG．
又ME?面A′CD，DG?平面A′CD，
∴ME∥平面A′CD．
点评：本题考查线面平行的判定定理，考查学生分析解决问题的能力，证明四边形DEMG是平行四边形是关键．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，其中有两解的是（ ）
| A、a=8，b=15，A=30° |
| B、a=30，b=25，A=150° |
| C、a=72，b=50，A=135° |
| D、a=18，b=16，A=60° |
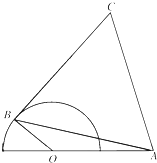如图，半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一点，以AB为一边作等边三角形ABC．