题目内容
设全集U=R，集合A={x|x＞0}，B={x|x＞1}，则A∩B= ．
考点：交集及其运算
专题：集合
分析：直接利用交集运算得答案．
解答：
解：∵A={x|x＞0}，B={x|x＞1}，
∴A∩B={x|x＞0}∩{x|x＞1}={x|x＞1}．
故答案为：{x|x＞1}．
∴A∩B={x|x＞0}∩{x|x＞1}={x|x＞1}．
故答案为：{x|x＞1}．
点评：本题考查了交集及其运算，是基础的计算题．
练习册系列答案
相关题目
已知函数f（x）=sin2x向左平移
个单位后，得到函数y=g（x），下列关于y=g（x）的说法正确的是（ ）
| π |
| 6 |
A、图象关于点（-
| ||||
B、图象关于x=-
| ||||
C、在区间[-
| ||||
D、在[-
|
设集合A={x∈Q|x＞-1}，则（ ）
| A、∅∉A | ||
B、
| ||
C、{
| ||
D、{
|
M是椭圆
+
=1上的点，F1、F2是椭圆的两个焦点，∠F1MF2=60°，则△F1MF2的面积等于（ ）
| x2 |
| 25 |
| y2 |
| 9 |
A、3
| ||
B、6
| ||
| C、3 | ||
D、2
|
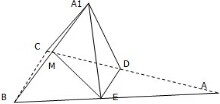已知在△ABC中，D，E分别为AC，AB的中点，沿DE将三角形ADE折起，使A到达A′的位置，若M是A′B的中点，求证：ME∥平面A′CD．