题目内容
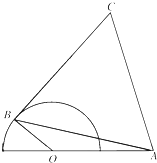 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.问:当点B在什么位置时,四边形OACB的面积最大?
考点:圆的切线的判定定理的证明
专题:立体几何
分析:在△AOB中,由已知OA=2,OB=1,设∠AOB=α,则可应用余弦定理将AB的长用α的三角函数表示出来,进而四边形OACB面积S=S△AOB+S△AB表示成为α的三角函数,再注意α∈(0,π),将三角函数化简成为y=Asin(ωx+φ)+B的形式,就可求得使四边形OACB面积最大的角α的值,从而就可确定点B的位置.
解答:
解:设∠AOB=α,(1分)
在△AOB中,由余弦定理得
AB2=OA2+OB2-2×OA×OBcos∠AOB
=12+22-2×1×2×cosα
=5-4cosα,.(4分)
于是,四边形OACB的面积为
S=S△AOB+S△ABC=
OA•OBsinα+
AB2 (6分)
=
×2×1×sinα+
(5-4cosα)
=sinα-
cosα+
=2sin(x-
)+
.(10分)
因为0<α<π,所以当α-
=
,α=
,
即∠AOB=
时,四边形OACB面积最大.(12分)
在△AOB中,由余弦定理得
AB2=OA2+OB2-2×OA×OBcos∠AOB
=12+22-2×1×2×cosα
=5-4cosα,.(4分)
于是,四边形OACB的面积为
S=S△AOB+S△ABC=
| 1 |
| 2 |
| ||
| 4 |
=
| 1 |
| 2 |
| ||
| 4 |
=sinα-
| 3 |
5
| ||
| 4 |
=2sin(x-
| π |
| 3 |
5
| ||
| 4 |
因为0<α<π,所以当α-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
即∠AOB=
| 5π |
| 6 |
点评:本题考查四边形面积最大时点的位置的确定,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合A={x∈Q|x>-1},则( )
| A、∅∉A | ||
B、
| ||
C、{
| ||
D、{
|
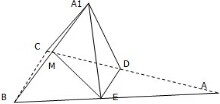 已知在△ABC中,D,E分别为AC,AB的中点,沿DE将三角形ADE折起,使A到达A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.
已知在△ABC中,D,E分别为AC,AB的中点,沿DE将三角形ADE折起,使A到达A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.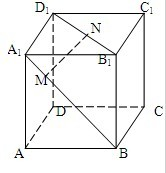 如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.
如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.