题目内容
在△ABC中，其中有两解的是（ ）
| A、a=8，b=15，A=30° |
| B、a=30，b=25，A=150° |
| C、a=72，b=50，A=135° |
| D、a=18，b=16，A=60° |
考点：正弦定理
专题：解三角形
分析：各项利用正弦定理列出关系式，把a，b，sinA的值代入求出sinB的值，即可做出判断．
解答：
解：A、∵a=8，b=15，A=30°，
∴由正弦定理
=
得：sinB=
=
=
，
∵a＜b，∴A＜B，
则B有两解，符合题意；
B、∵a=30，b=25，A=150°，
∴由正弦定理
=
得：sinB=
=
=
，
∵A为钝角，
∴B只有一解，不合题意；
C、∵a=72，b=50，A=135°，
∴由正弦定理
=
得：sinB=
=
=
，
∵A为钝角，∴B只有一解，不合题意；
D、∵a=18，b=20，A=60°，
∴由正弦定理
=
得：sinB=
=
=
，
∵a＞b，∴A＞B，即B＜60°，此时三角形无解，
故选：A．
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| a |
15×
| ||
| 8 |
| 15 |
| 16 |
∵a＜b，∴A＜B，
则B有两解，符合题意；
B、∵a=30，b=25，A=150°，
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| a |
25×
| ||
| 30 |
| 5 |
| 12 |
∵A为钝角，
∴B只有一解，不合题意；
C、∵a=72，b=50，A=135°，
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| a |
50×
| ||||
| 72 |
25
| ||
| 72 |
∵A为钝角，∴B只有一解，不合题意；
D、∵a=18，b=20，A=60°，
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| a |
20×
| ||||
| 18 |
5
| ||
| 9 |
∵a＞b，∴A＞B，即B＜60°，此时三角形无解，
故选：A．
点评：此题考查了正弦定理，熟练掌握正弦定理是解本题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
方程x2-3x+1=0的两根e1和e2可以分别为（ ）
| A、椭圆与双曲线的离心率 |
| B、两条抛物线的离心率 |
| C、两个椭圆的离心率 |
| D、椭圆与抛物线的离心率 |
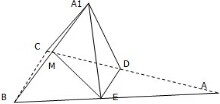已知在△ABC中，D，E分别为AC，AB的中点，沿DE将三角形ADE折起，使A到达A′的位置，若M是A′B的中点，求证：ME∥平面A′CD．