题目内容
已知:f(x)=(a-2)x2+2(a-2)x-4,
(1)当x∈R时,恒有f(x)<0,求a的取值范围;
(2)当x∈[1,3)时,恒有f(x)<0,求a的取值范围;
(3)当x∈(1,3)时,恰有f(x)<mx-7成立,求a,m的值.
(1)当x∈R时,恒有f(x)<0,求a的取值范围;
(2)当x∈[1,3)时,恒有f(x)<0,求a的取值范围;
(3)当x∈(1,3)时,恰有f(x)<mx-7成立,求a,m的值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)分a=2时,和a<2时两种情况进行讨论,当a<2时,根据判别式小于0即可.
(2)分a=2时,和a≠2时两种情况进行讨论,分别求出a的范围后,综合讨论结果,可得答案.
(3)结合二次函数的图象和性质分类讨论,综合讨论结果,可得答案.
(2)分a=2时,和a≠2时两种情况进行讨论,分别求出a的范围后,综合讨论结果,可得答案.
(3)结合二次函数的图象和性质分类讨论,综合讨论结果,可得答案.
解答:
解:(1)当a=2时,f(x)=-4<0,故当x∈R时,恒有f(x)<0,
当
⇒-2<a<2,
综上所述a的取值范围(-2,2].
(2)由(1)得a=2,成立,当a≠2,对称轴x=-1
∴
或
⇒a<2或2<a≤
∴综上所述a的取值范围(-∞,
].
(3)∵f(x)<mx-7,
∴f(x)-mx+7<0,
即(a-2)x2+(2a-4-m)x+3<0,
令g(x)=(a-2)x2+(2a-4-m)x+3<0
∵x∈(1,3)时,恰有f(x)<mx-7成立
∴
⇒
⇒
.
故a=3,m=6.
当
|
综上所述a的取值范围(-2,2].
(2)由(1)得a=2,成立,当a≠2,对称轴x=-1
∴
|
|
| 34 |
| 15 |
∴综上所述a的取值范围(-∞,
| 34 |
| 15 |
(3)∵f(x)<mx-7,
∴f(x)-mx+7<0,
即(a-2)x2+(2a-4-m)x+3<0,
令g(x)=(a-2)x2+(2a-4-m)x+3<0
∵x∈(1,3)时,恰有f(x)<mx-7成立
∴
|
|
|
故a=3,m=6.
点评:本题考查的知识点是函数恒成立问题,函数的最值,其中将恒成立问题转化为最值问题是解答此类问题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}在n≥7时为递增数列,则实数λ的取值范围为( )
| A、(-15,+∞) |
| B、[-15,+∞) |
| C、[-16,+∞) |
| D、(-16,+∞) |
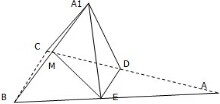 已知在△ABC中,D,E分别为AC,AB的中点,沿DE将三角形ADE折起,使A到达A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.
已知在△ABC中,D,E分别为AC,AB的中点,沿DE将三角形ADE折起,使A到达A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.