题目内容
若f（1-x）=x2，则f（1）= ．
考点：函数的值
专题：函数的性质及应用
分析：根据函数的解析式，进行转化即可．
解答：
解：∵f（1-x）=x2，
∴f（1）=f（1-0）=02=0，
故答案为：0
∴f（1）=f（1-0）=02=0，
故答案为：0
点评：本题主要考查函数值的计算，比较基础．
练习册系列答案
相关题目
下列各图表示两个变量x、y的对应关系，则下列判断正确的是（ ）
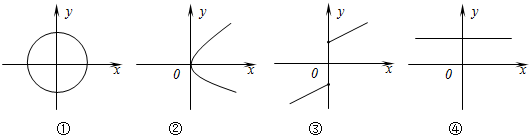
| A、都表示映射，都表示y是x的函数 |
| B、仅③表示y是x的函数 |
| C、仅④表示y是x的函数 |
| D、都不能表示y是x的函数 |
函数y=cos2（x-
）-cos2（x+
）是（ ）
| π |
| 4 |
| π |
| 4 |
| A、最小正周期为π的奇函数 | ||
| B、最小正周期为π的偶函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
已知函数f（x）=sin2x向左平移
个单位后，得到函数y=g（x），下列关于y=g（x）的说法正确的是（ ）
| π |
| 6 |
A、图象关于点（-
| ||||
B、图象关于x=-
| ||||
C、在区间[-
| ||||
D、在[-
|
设集合A={x∈Q|x＞-1}，则（ ）
| A、∅∉A | ||
B、
| ||
C、{
| ||
D、{
|
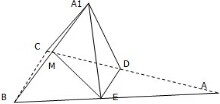已知在△ABC中，D，E分别为AC，AB的中点，沿DE将三角形ADE折起，使A到达A′的位置，若M是A′B的中点，求证：ME∥平面A′CD．