题目内容
现有4名教师参加说课比赛,共有4道备选题目,若每位教师从中有放回地随机选出一道题目进行说课,其中恰有一道题目没有被这4位教师选中的情况有 .
考点:计数原理的应用
专题:排列组合
分析:利用间接法,先确定4个老师无遗漏的选择,再去掉恰好2、3、4道题目未被选的情况,即可得出结论
解答:
解:由题意,每个老师都有4种选择,所以4个老师无遗漏的选择是44=256种,
其中恰好2道题目未被选的有
(
+
)=84、恰好3道目未被选(四人选了同一道题,有4种)、恰好0道题目未被选的(四道题都被选,有
=24种).
故共有256-84-4-24=144,
其中恰好2道题目未被选的有
| C | 2 4 |
| C | 3 4 |
| A | 2 2 |
| C | 2 4 |
| A | 4 4 |
故共有256-84-4-24=144,
点评:本题考查计数原理的应用,考查间接法,解题的关键是去掉恰好2、3、4道题目未被选的情况,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}在n≥7时为递增数列,则实数λ的取值范围为( )
| A、(-15,+∞) |
| B、[-15,+∞) |
| C、[-16,+∞) |
| D、(-16,+∞) |
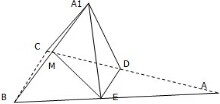 已知在△ABC中,D,E分别为AC,AB的中点,沿DE将三角形ADE折起,使A到达A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.
已知在△ABC中,D,E分别为AC,AB的中点,沿DE将三角形ADE折起,使A到达A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.