题目内容
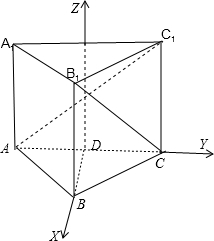
设正三棱柱ABC-A1B1C1的底面边长为a,点P,Q在A1C上,点R,S在BC1上,且四面体PQRS为正四面体,则该正四面体棱长为 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:首先建立空间直角坐标系证明异面直线AC1和B1C垂直,进一步求出该异面直线间的距离,最后利用正四面体的性质求出相关的结论及正四面体的边长.
解答:
 解:设正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
解:设正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
a,
可利用空间直角坐标系:D-XYZ,
则:D(0,0,0),C(0,
,0),B(
a,0,0),B1(
a,0,
a),A(0,-
,0),C1(0,
,
a),
利用向量的数量积解得:
•
=0,
所以异面直线AC1和B1C垂直,
且AC1和B1C距离为:中点的连线,
根据中位线定理得:距离长为
,
点P,Q在A1C上,点R,S在BC1上,且四面体PQRS为正四面体,
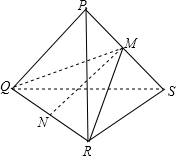
根据四面体得到:MN是异面直线PS和QR之间的距离.
即异面直线AC1和B1C之间的距离.
设正四面体的边长为:RS=x,
进一步解得:MR=
x,MS=
x,
利用勾股定理解得:MN=
x,
令:
x=
,
所以:x=
a,
即正四面体的边长为:
a,
故答案为:
a.

 解:设正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
解:设正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
| ||
| 2 |
可利用空间直角坐标系:D-XYZ,
则:D(0,0,0),C(0,
| a |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
利用向量的数量积解得:
| AC1 |
| B1C |
所以异面直线AC1和B1C垂直,
且AC1和B1C距离为:中点的连线,
根据中位线定理得:距离长为
| a |
| 2 |
点P,Q在A1C上,点R,S在BC1上,且四面体PQRS为正四面体,
根据四面体得到:MN是异面直线PS和QR之间的距离.
即异面直线AC1和B1C之间的距离.
设正四面体的边长为:RS=x,
进一步解得:MR=
| ||
| 2 |
| 1 |
| 2 |
利用勾股定理解得:MN=
| ||
| 2 |
令:
| ||
| 2 |
| a |
| 2 |
所以:x=
| ||
| 2 |
即正四面体的边长为:
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查的知识点:正三棱柱与正四面体的性质,异面直线间的距离,空间直角坐标系的应用,向量垂直的充要条件及相关的运算问题.

练习册系列答案
相关题目