题目内容
函数f（x）=
的定义域为 ．
| 1 |
| ln(x-2) |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：对数的真数大于0，分母不为零，可求其定义域．
解答：
解：要使函数有意义，必有x-2＞0且x-2≠1，
即x＞2且x≠3．
故答案为：{x|x＞2，x≠3}）；
即x＞2且x≠3．
故答案为：{x|x＞2，x≠3}）；
点评：本题考查对数函数的定义域的求法，解题时注意负数和0没有对数，是基础题．
练习册系列答案
相关题目
已知函数g（x）=(
)x与函数y=f（x）的图象关于直线y=x对称，若a=g（0.2），b=f（2），c=f（0.2），则（ ）
| 1 |
| 3 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、a＜c＜b |
| D、c＜b＜a |
阅读程序框图，运行相应的程序，输出的结果为（ ）
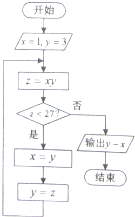
| A、6 | B、-6 | C、0 | D、18 |
在△ABC中，若sinA+cosA=
，则tanA=（ ）
| 1 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知函数f（x）=
，若f（-x）=2，则x=（ ）
|
A、-
| ||
B、-
| ||
C、
| ||
D、
|