题目内容
空间中有一条线段PQ的三视图,俯视图是长度为1的线段,侧视图是长度为2的线段,则线段PQ长的取值范围 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:利用特殊的图象把问题进行转化,利用长方体的边与边的关系求出PQ2≤(a2+b2)+(c2+b2)=5,进一步求出PQ2≥b2+c2=4,最后求出结论.
解答:
解:设长方体的边长为:a、b、c,
线段PQ的三视图,俯视图是长度为1的线段,侧视图是长度为2的线段
则:a2+b2=1,b2+c2=4
PQ2≤(a2+b2)+(c2+b2)=5
PQ2≥b2+c2=4
即:5≥PQ2≥4
≥PQ≥2
故答案为:
≥PQ≥2

线段PQ的三视图,俯视图是长度为1的线段,侧视图是长度为2的线段
则:a2+b2=1,b2+c2=4
PQ2≤(a2+b2)+(c2+b2)=5
PQ2≥b2+c2=4
即:5≥PQ2≥4
| 5 |
故答案为:
| 5 |

点评:本题考查的知识要点:三视图与立体图象之间的转化,三角形的边与边的关系.及相关的运算问题.属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
阅读程序框图,运行相应的程序,输出的结果为( )
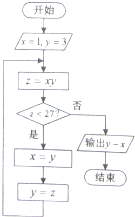

| A、6 | B、-6 | C、0 | D、18 |
化(
) -
的结果是( )
| 27 |
| 125 |
| 1 |
| 3 |
| A、3 | ||
| B、5 | ||
C、
| ||
D、
|
已知函数f(x)=
,若f(-x)=2,则x=( )
|
A、-
| ||
B、-
| ||
C、
| ||
D、
|