题目内容
18.若集合M={y|y=x4,x∈(-1,0)},集合$N=\left\{{x|y=ln\frac{x}{x-1}}\right\}$,则下列各式中正确的是( )| A. | M?N | B. | N?M | C. | M∩N=ϕ | D. | M=N |
分析 化简集合M、N,根据集合的运算法则即可得出结论.
解答 解:集合M={y|y=x4,x∈(-1,0)}={y|0<y<1}=(0,1),
集合$N=\left\{{x|y=ln\frac{x}{x-1}}\right\}$={x|$\frac{x}{x-1}$>0}={x|x<0或x>1}=(-∞,0)∪(1,+∞),
∴M∩N=∅.
故选:C.
点评 本题考查了集合的化简与运算问题,是基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
9.将函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{3}$个单位长度后,所得函数g(x)的图象关于原点对称,则函数f(x)在$[{0,\frac{π}{2}}]$的最大值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
3.已知双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$,则其焦距为( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $\sqrt{13}$ | D. | $2\sqrt{13}$ |
2.函数f(x)=3x2+ex-2(x<0)与g(x)=3x2+ln(x+t)图象上存在关于y轴对称的点,则t的取值范围是( )
| A. | (-∞,$\frac{1}{e}$) | B. | (-∞,e) | C. | (-e,$\frac{1}{e}$) | D. | (-$\frac{1}{e}$,e) |
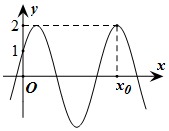 已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.