题目内容
15.定义在R上的奇函数f(x)在(-∞,0)上递增,f(2)=1,则满足|f(log${\;}_{\frac{1}{2}}$x)|>1的x的取值范围是( )| A. | ($\frac{1}{4}$,4) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{2}$)∪(2,+∞) | D. | (0,$\frac{1}{4}$)∪(4,+∞) |
分析 由题意可得f(x)在(0,+∞)上也单调递增,并求得f(-2)=-f(2)=-1.然后由|f(log${\;}_{\frac{1}{2}}$x)|>1得|f(log2x)|>1,去绝对值后由函数单调性转化为对数不等式求解.
解答 解:∵定义在R上的奇函数f(x)在(-∞,0)上递增,
∴f(x)在(0,+∞)上也单调递增,
又f(2)=1,∴f(-2)=-f(2)=-1.
由|f(log${\;}_{\frac{1}{2}}$x)|>1,得|f(-log2x)|>1,即|-f(log2x)|>1,
∴|f(log2x)|>1,得f(log2x)>1或f(log2x)<-1,
由f(log2x)>1,得f(log2x)>f(2),即log2x>2,得x>4;
由f(log2x)<-1,f(log2x)<f(-2),即log2x<-2,得0<x<$\frac{1}{4}$.
∴x的取值范围是(0,$\frac{1}{4}$)∪(4,+∞).
故选:D.
点评 本题考查函数的性质及其应用,考查对数不等式的解法,是中档题.

练习册系列答案
相关题目
3.已知双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$,则其焦距为( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $\sqrt{13}$ | D. | $2\sqrt{13}$ |
20.已知向量$\overrightarrow a$与$\overrightarrow b$不共线,$\overrightarrow{AB}=\overrightarrow a+m\overrightarrow b$,$\overrightarrow{AC}=n\overrightarrow a+\overrightarrow b$(m,n∈R),则$\overrightarrow{AB}$与$\overrightarrow{AC}$共线的条件是( )
| A. | m+n=0 | B. | m-n=0 | C. | mn+1=0 | D. | mn-1=0 |
19.函数f(x)=x|x|.若存在x∈[1,+∞),使得f(x-2k)-k<0,则k的取值范围是( )
| A. | (2,+∞) | B. | (1,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{4}$,+∞) |
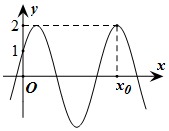 已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.