题目内容
7名师生从左到右站成一排照相留念,1名老师,4名男生,2名女生,在下列情况,名有多少种不同的站法?
(1)2名女生必须相邻而站;
(2)4名男生互不相邻;
(3)甲生甲站在男生乙的左边(不一定相邻);
(4)甲生甲不站最左边,女生乙不站最右边.
(1)2名女生必须相邻而站;
(2)4名男生互不相邻;
(3)甲生甲站在男生乙的左边(不一定相邻);
(4)甲生甲不站最左边,女生乙不站最右边.
考点:计数原理的应用
专题:排列组合
分析:(1)两个女生必须相邻而站;把两个女生看做一个元素,则共有6个元素进行全排列,还有女生内部的一个排列.
(2)4名男生互不相邻,应用插空法,要老师和女生先排列,形成四个空再排男生.
(3)男生甲和男生乙的位置只有两种顺序,先排,再除以顺序数即可.
(4)分两类,男生甲在最右边,男生甲在不在最右边,根据分类计数原理即可得到答案.
(2)4名男生互不相邻,应用插空法,要老师和女生先排列,形成四个空再排男生.
(3)男生甲和男生乙的位置只有两种顺序,先排,再除以顺序数即可.
(4)分两类,男生甲在最右边,男生甲在不在最右边,根据分类计数原理即可得到答案.
解答:
解:(1)∵两个女生必须相邻而站,∴把两个女生看做一个元素,
则共有6个元素进行全排列,还有女生内部的一个排列共有A66A22=1440.
(2)∵4名男生互不相邻,∴应用插空法,
要老师和女生先排列,形成四个空再排男生共有A33A44=144.
(3)∵男生甲站在男生乙的左边,∴男生甲和男生乙的位置只有两种顺序,故有
A77=2520..
(4)分两类,男生甲在最右边,有A66=720.男生甲在不在最右边,有A51A51A55=3000,
根据分类计数原理共有720+3000=3720.
则共有6个元素进行全排列,还有女生内部的一个排列共有A66A22=1440.
(2)∵4名男生互不相邻,∴应用插空法,
要老师和女生先排列,形成四个空再排男生共有A33A44=144.
(3)∵男生甲站在男生乙的左边,∴男生甲和男生乙的位置只有两种顺序,故有
| 1 |
| 2 |
(4)分两类,男生甲在最右边,有A66=720.男生甲在不在最右边,有A51A51A55=3000,
根据分类计数原理共有720+3000=3720.
点评:站队问题是排列组合中的典型问题,解题时,要先排限制条件多的元素,把排列问题包含在实际问题中,解题的关键是看清题目的实质,把实际问题转化为数学问题,解出结果以后再还原为实际问题.

练习册系列答案
相关题目
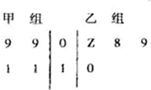 如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以Z表示.
如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以Z表示.