题目内容
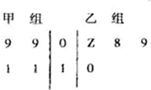 如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以Z表示.
如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以Z表示.(1)如果Z=8,求乙组同学植树棵数的平均数和方差;
(2)如果Z=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
考点:古典概型及其概率计算公式,茎叶图
专题:概率与统计
分析:(1)当Z=8时,由茎叶图知,乙组同学的植树棵数是8,8,9,10,由此能求出乙组同学植树棵数的平均数和方差.
(2)Z=9时,甲组四名同学植树棵数分别为9,9,11,11,乙组四名同学植树棵数分别为9,8,9,10,
分别从甲、乙两组中随机取一名同学,所有可能结果n=4×4=16,选出这两名同学的植树总棵数为19,包含基本事件个数m=4,由此能求出这两名同学的植树总棵数为19的概率.
(2)Z=9时,甲组四名同学植树棵数分别为9,9,11,11,乙组四名同学植树棵数分别为9,8,9,10,
分别从甲、乙两组中随机取一名同学,所有可能结果n=4×4=16,选出这两名同学的植树总棵数为19,包含基本事件个数m=4,由此能求出这两名同学的植树总棵数为19的概率.
解答:
解:(1)当Z=8时,由茎叶图知,
乙组同学的植树棵数是8,8,9,10,
∴
=
=
,
S2=
[(8-
)2+(8-
)2+(9-
)2+(10-
)2]=
.
(2)Z=9时,甲组四名同学植树棵数分别为9,9,11,11,
乙组四名同学植树棵数分别为9,8,9,10,
分别从甲、乙两组中随机取一名同学,
所有可能结果n=4×4=16,
选出这两名同学的植树总棵数为19,包含基本事件个数m=4,
∴这两名同学的植树总棵数为19的概率:
p=
=
=
.
乙组同学的植树棵数是8,8,9,10,
∴
. |
| x |
| 8+8+9+10 |
| 4 |
| 35 |
| 4 |
S2=
| 1 |
| 4 |
| 35 |
| 4 |
| 35 |
| 4 |
| 35 |
| 4 |
| 35 |
| 4 |
| 11 |
| 16 |
(2)Z=9时,甲组四名同学植树棵数分别为9,9,11,11,
乙组四名同学植树棵数分别为9,8,9,10,
分别从甲、乙两组中随机取一名同学,
所有可能结果n=4×4=16,
选出这两名同学的植树总棵数为19,包含基本事件个数m=4,
∴这两名同学的植树总棵数为19的概率:
p=
| m |
| n |
| 4 |
| 16 |
| 1 |
| 4 |
点评:本题考查平均数和方差的求法,考查概率的求法是基础题,解题时要认真审题,注意茎叶图的合理运用.

练习册系列答案
相关题目
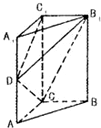 如图,直三棱柱ABC-A1B1C1中,AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.
如图,直三棱柱ABC-A1B1C1中,AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.