题目内容
已知5个数成等差数列,它们的和为5,平方和为
,求这个数列.
| 85 |
| 9 |
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:设这5个数分别为a-2d,a-d,a,a+d,a+2d,由已知得(a-2d)+(a-d)+a+(a+d)+(a+2d)=5,(a-2d)2+(a-d)2+a2+(a+d)2+(a+2d)2=
,由此能求出结果.
| 85 |
| 9 |
解答:
解:由已知5个数成等差数列,
设这5个数分别为a-2d,a-d,a,a+d,a+2d,
(a-2d)+(a-d)+a+(a+d)+(a+2d)=5,
5a=5,
a=1,
(a-2d)2+(a-d)2+a2+(a+d)2+(a+2d)2=
,
5a2+10d2=85/9,
a=1代入,整理,得
d2=
,
d=
或d=-
,
d=
时,a-2d=1-
=-
,a-d=1-
=
,a+d=1+
=
,a+2d=1+
=
;
d=-
时,a-2d=1+
=
,a-d=1+
=
,a+d=1-
=
,a+2d=1-
=-
.
这5个数分别为-
,
,1,
,
;或
,
,1,
,-
.
设这5个数分别为a-2d,a-d,a,a+d,a+2d,
(a-2d)+(a-d)+a+(a+d)+(a+2d)=5,
5a=5,
a=1,
(a-2d)2+(a-d)2+a2+(a+d)2+(a+2d)2=
| 85 |
| 9 |
5a2+10d2=85/9,
a=1代入,整理,得
d2=
| 4 |
| 9 |
d=
| 2 |
| 3 |
| 2 |
| 3 |
d=
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
d=-
| 2 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
这5个数分别为-
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 7 |
| 3 |
| 7 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查等差数列的求法,是基础题,解题时要认真审题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
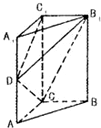 如图,直三棱柱ABC-A1B1C1中,AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.
如图,直三棱柱ABC-A1B1C1中,AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.