题目内容
函数f(x)=2sinωx在[-
,
]上单调递增,那么ω的取值范围是( )
| π |
| 6 |
| π |
| 4 |
A、(0,
| ||
| B、(0,2] | ||
| C、[-3,2] | ||
| D、[-2,2] |
考点:正弦函数的图象
专题:计算题,三角函数的图像与性质
分析:根据正弦型函数的性质,可得在ω>0时,区间[-
,
]是函数y=2sinωx的一个单调递增区间,结合已知中函数y=2sinωx(ω>0)在[-
,
]上单调递增,推出一个关于ω的不等式组,解不等式组,即可求出实数ω的取值范围.
| π |
| 2ω |
| π |
| 2ω |
| π |
| 6 |
| π |
| 4 |
解答:
解:由正弦函数的性质,在ω>0时,
当x=-
,函数取得最小值,x=
函数取得最大值,
所以,区间[-
,
]是函数y=2sinωx的一个单调递增区间,
若函数y=2sinωx(ω>0)在[-
,
]上单调递增
则-
≤-
且
≥
解得0<ω≤2
故选:B.
当x=-
| π |
| 2ω |
| π |
| 2ω |
所以,区间[-
| π |
| 2ω |
| π |
| 2ω |
若函数y=2sinωx(ω>0)在[-
| π |
| 6 |
| π |
| 4 |
则-
| π |
| 2ω |
| π |
| 6 |
| π |
| 2ω |
| π |
| 4 |
解得0<ω≤2
故选:B.
点评:本题考查的知识点是正弦型函数的单调性,其中根据正弦型函数的性质,得到ω>0时,区间[-
,
]是函数y=2sinωx的一个单调递增区间,进而结合已知条件构造一个关于ω的不等式组,是解答本题的关键,属于中档题.
| π |
| 2ω |
| π |
| 2ω |

练习册系列答案
相关题目
已知向量
=(1,2),(
+
)∥
,则
可以为( )
| a |
| a |
| b |
| b |
| b |
| A、(1,2) |
| B、(1,-2) |
| C、(2,1) |
| D、(2,-1) |
根据表格中的数据,可以判定方程ex-x-6=0的一个根所在的区间为( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
使函数y=2sin(2x+φ+
)为奇函数,且在[0,
]上是减函数的φ的一个值是( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
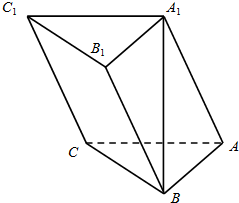 在三棱柱ABC-A1B1C1中,AB⊥AC,A1B⊥平面ABC,且AB=AC=A1B=2.
在三棱柱ABC-A1B1C1中,AB⊥AC,A1B⊥平面ABC,且AB=AC=A1B=2.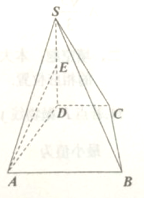 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和CD,侧棱SD⊥底面ABCD,且SD=AD=AB=2CD,点E为棱SD的中点.求异面直线AE和SB所成角的余弦值.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和CD,侧棱SD⊥底面ABCD,且SD=AD=AB=2CD,点E为棱SD的中点.求异面直线AE和SB所成角的余弦值.