题目内容
使函数y=2sin(2x+φ+
)为奇函数,且在[0,
]上是减函数的φ的一个值是( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:根据正弦函数的性质求得φ的集合,根据单调性确定φ的值.
解答:
解:∵函数y=2sin(2x+φ+
)为奇函数,
∴φ+
=kπ,k∈Z,即φ=kπ-
,
∵在[0,
]上是减函数,
∴φ=kπ-
,(k为奇数),
∴
为φ的一个值,
故选:C.
| π |
| 3 |
∴φ+
| π |
| 3 |
| π |
| 3 |
∵在[0,
| π |
| 4 |
∴φ=kπ-
| π |
| 3 |
∴
| 2π |
| 3 |
故选:C.
点评:本题主要考查了正弦函数的图象与性质,考查了学生分析和推理能力和数形结合思想的灵活运用,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
已知集合A={x|x2-2x<0},B={x|1<x<3},那么A∩B=( )
| A、{x|0<x<2} |
| B、{x|1<x<2} |
| C、{x|0<x<3} |
| D、{x|1<x<3} |
函数f(x)=2sinωx在[-
,
]上单调递增,那么ω的取值范围是( )
| π |
| 6 |
| π |
| 4 |
A、(0,
| ||
| B、(0,2] | ||
| C、[-3,2] | ||
| D、[-2,2] |
关于循环结构的论述正确的是( )


| A、①是直到型循环结构④是当型循环结构 |
| B、①是直到型循环结构③是当型循环结构 |
| C、②是直到型循环结构④是当型循环结构 |
| D、④是直到型循环结构①是当型循环结构 |
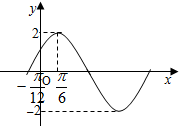 已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,|φ|<