Question

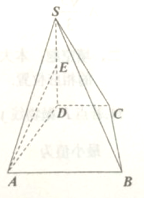如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AD垂直于AB和CD，侧棱SD⊥底面ABCD，且SD=AD=AB=2CD，点E为棱SD的中点．求异面直线AE和SB所成角的余弦值．

Answer 1

考点：异面直线及其所成的角

专题：空间角

分析：以D为原点，DA为x轴，DC为y轴，DS为z轴，建立空间直角坐标系，利用向量法能求出异面直线AE和SB所成角的余弦值．

解答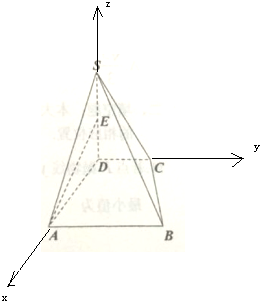： 解：以D为原点，DA为x轴，DC为y轴，DS为z轴，
建立空间直角坐标系，
设SD=AD=AB=2CD=2，由已知得A（2，0，0），
E（0，0，1），S（0，0，2），B（2，2，0），

AE

=（-2，0，1），

SB

=（2，2，-2），
∴|cos＜

AE

，

SB

＞|=|

-4+0-2

4+1 • 4+4+4

|=

15

5

．
∴异面直线AE和SB所成角的余弦值为

15

5

．

点评：本题考查异面直线所成角的余弦值的求法，是基础题，解题时要注意空间思维能力的培养．