题目内容
在直角坐标系xOy中,设点A(-1,0),B(1,0),Q为△ABC的外心.已知
+2
=0,OG∥AB.
(1)求点C的轨迹Γ的方程
(2)设经过f(0,
)的直线交轨迹Γ与E,H,直线EH与直线l:y=
交于点M,点P是直线y=
上异于点F的任意一点.若直线PE,PH,PM的斜率分别为k1,k2,k3,问是否存在实数t,使得
+
=
,若存在,求t的值;若不存在,说明理由.
| CG |
| OG |
(1)求点C的轨迹Γ的方程
(2)设经过f(0,
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
| 1 |
| k1 |
| 1 |
| k2 |
| t |
| k3 |
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)设C(x,y),
+2
=
,可得G(
,
),Q(0,
),根据|QA|=|QC|,即可得出.
(2)当直线EF的斜率不存在时,t=2.当直线EF的斜率存在时,设斜率为k.则直线EH的方程为y=kx+
,点M的坐标为(
,
).把直线方程代入椭圆方程可得(k2+3)x2+2
kx-1=0,设E(x1,y1),F(x2,y2),P(a,
)(a≠0).利用根与系数的关系可得
=
=
,
=
,
=
-
a.又
+
=
,即可得出.
| CG |
| OG |
| 0 |
| x |
| 3 |
| y |
| 3 |
| y |
| 3 |
(2)当直线EF的斜率不存在时,t=2.当直线EF的斜率存在时,设斜率为k.则直线EH的方程为y=kx+
| 2 |
| ||
| 2k |
3
| ||
| 2 |
| 2 |
| 2 |
| 1 |
| k1 |
| x1-a | ||
y1-
|
| x1-a |
| kx1 |
| 1 |
| k2 |
| x2-a |
| kx2 |
| 1 |
| k3 |
| 1 |
| k |
| 2 |
| 1 |
| k1 |
| 1 |
| k2 |
| t |
| k3 |
解答:
解:(1)设C(x,y),
+2
=
,则G(
,
),Q(0,
),
根据|QA|=|QC|,
可得x2+
=1(y≠0).
(2)当直线EF的斜率不存在时,t=2.
当直线EF的斜率存在时,设斜率为k.则直线EH的方程为y=kx+
,点M的坐标为(
,
).
把直线方程代入椭圆方程可得(k2+3)x2+2
kx-1=0,设E(x1,y1),F(x2,y2),P(a,
)(a≠0).
则x1+x2=
,x1x2=
,
∴
=
=
,
=
,
=
-
a.
又∵
+
=
,
∴
+
=
-2
a.
故存在常数t=2满足条件.
| CG |
| OG |
| 0 |
| x |
| 3 |
| y |
| 3 |
| y |
| 3 |
根据|QA|=|QC|,
可得x2+
| y2 |
| 3 |
(2)当直线EF的斜率不存在时,t=2.
当直线EF的斜率存在时,设斜率为k.则直线EH的方程为y=kx+
| 2 |
| ||
| 2k |
3
| ||
| 2 |
把直线方程代入椭圆方程可得(k2+3)x2+2
| 2 |
| 2 |
则x1+x2=
-2
| ||
| k2+3 |
| -1 |
| k2+3 |
∴
| 1 |
| k1 |
| x1-a | ||
y1-
|
| x1-a |
| kx1 |
| 1 |
| k2 |
| x2-a |
| kx2 |
| 1 |
| k3 |
| 1 |
| k |
| 2 |
又∵
| 1 |
| k1 |
| 1 |
| k2 |
| t |
| k3 |
∴
| x1-a |
| kx1 |
| x2-a |
| kx2 |
| 2 |
| k |
| 2 |
故存在常数t=2满足条件.
点评:本题综合考查了椭圆与圆的标准方程及其性质、直线与椭圆相切转化为方程联立可得根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于难题.题目应该为CG+2QG=0 QG平行于AB

练习册系列答案
相关题目
已知函数f(x)=
x3+ax+4则“a>0”是“f(x)在R上单调递增”的( )
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分,也不必要条件 |
函数f(x)=2sinωx在[-
,
]上单调递增,那么ω的取值范围是( )
| π |
| 6 |
| π |
| 4 |
A、(0,
| ||
| B、(0,2] | ||
| C、[-3,2] | ||
| D、[-2,2] |
关于循环结构的论述正确的是( )


| A、①是直到型循环结构④是当型循环结构 |
| B、①是直到型循环结构③是当型循环结构 |
| C、②是直到型循环结构④是当型循环结构 |
| D、④是直到型循环结构①是当型循环结构 |
在每条棱长都相等的底面是菱形的直棱柱ABCD-A1B1C1D1中,∠ABC=
,侧棱AA1与对角线BD1所成的角为θ,则θ为( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
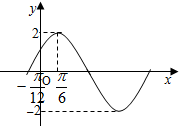 已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,|φ|<