题目内容
13．
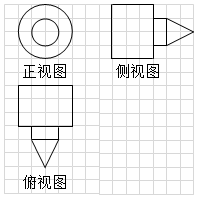放烟花是逢年过节一种传统庆祝节日的方式．已知一种烟花模型的三视图如图中的粗实线所示，网格纸上小正方形的边长为1，则该烟花模型的表面积为（| A． | $（18+\sqrt{3}）π$ | B． | $（21+\sqrt{3}）π$ | C． | $（18+\sqrt{5}）π$ | D． | $（21+\sqrt{5}）π$ |
分析 利用三视图判断几何体的形状，利用三视图的数据求解几何体的表面积即可．
解答 解：由三视图可知几何体是半径为2，高为3的圆柱，与半径为1，高为1的圆柱，以及底面半径为1，高为2的圆锥，组成的几何体．几何体的表面积为：2×4π-π+3×4π+2π×1+$\frac{1}{2}×2π×\sqrt{5}$=（21+$\sqrt{5}$）π．
故选：D．
点评 本题考查三视图求解几何体的表面积，判断几何体的形状是解题的关键．
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
4．
已知函数f（x）=ax3+bx2+c，其导函数f'（x）的图象如图，则函数f（x）的极小值为（ ）
已知函数f（x）=ax3+bx2+c，其导函数f'（x）的图象如图，则函数f（x）的极小值为（ ）| A． | c | B． | a+b+c | C． | 8a+4b+c | D． | 3a+2b |
3．已知抛物线y2=2px（p＞0）的焦点为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，且其准线被该双曲线截得的弦长是$\frac{2}{3}$b，则该双曲线的离心率为（ ）
| A． | $\frac{13}{9}$ | B． | $\frac{10}{9}$ | C． | $\frac{\sqrt{13}}{3}$ | D． | $\frac{\sqrt{10}}{3}$ |