题目内容
1.在二项式(x2+$\frac{1}{x}}$)5的展开式中,含x项的系数是a,则${∫}_{1}^{a}$x-1dx=ln10.分析 根据二项式${({{x^2}+\frac{1}{x}})^5}$的展开式中,含x项的系数是a,求出a的值.根据定积分公式求解定积分即可.
解答 解:二项式为${({{x^2}+\frac{1}{x}})^5}$,
由通项公式可得:Tr+1=${C}_{5}^{r}({x}^{-1})^{r}({x}^{2})^{5-r}$,
∵含x项,
∴r=3,
∴含x项的系数为${C}_{5}^{3}(1)^{3}$=10.
即a=10.
那么$\int_a^{10}{\;}{x^{-1}}dx$=${∫}_{10}^{10}{x}^{-1}{d}_{x}$=lnx|$\left.\begin{array}{l}{10}\\{1}\end{array}\right.$=ln10.
故答案为:ln10.
点评 本题主要考查二项式定理通项公式的应用,和定积分的计算.属于基础题.

练习册系列答案
相关题目
6.下列命题中:
①若a∈R,则(a+1)i是纯虚数;
②若a,b∈R且a>b,则a+i3>b+i2;
③若(x2-1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④两个虚数不能比较大小.
其中,正确命题的序号是( )
①若a∈R,则(a+1)i是纯虚数;
②若a,b∈R且a>b,则a+i3>b+i2;
③若(x2-1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④两个虚数不能比较大小.
其中,正确命题的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
12.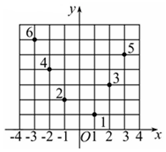 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )
 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )| A. | 2 011 | B. | 1 006 | C. | 1 005 | D. | 1 003 |
9.大前提:若函数f(x)是奇函数,则f(0)=0,小前提:$g(x)=\frac{1}{x}$是奇函数,结论:g(0)=0,则该推理过程( )
| A. | 正确 | B. | 因大前提错误导致结论出错 | ||
| C. | 因小前提导致结论出错 | D. | 因推理形式错误导致结论出错 |
13.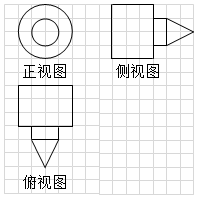 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(| A. | $(18+\sqrt{3})π$ | B. | $(21+\sqrt{3})π$ | C. | $(18+\sqrt{5})π$ | D. | $(21+\sqrt{5})π$ |
10.定义在R上的奇函数f(x)对任意x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$,若实数m,n满足f(m2+4m+12)+f(n2-6n)<0,则|m-2n-4|的取值范围为( )
| A. | $[\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1]$ | B. | $(\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1)$ | C. | $[12-\sqrt{5},12+\sqrt{5}]$ | D. | $(12-\sqrt{5},12+\sqrt{5})$ |