题目内容
5.当正数a,b,满足$\frac{4}{a+5b}+\frac{1}{3a+2b}=6$时,则4a+7b的最小值$\frac{3}{2}$.分析 由题意可知:4a+7b=$\frac{1}{6}$(4a+7b)×($\frac{4}{a+5b}$+$\frac{1}{3a+2b}$)=$\frac{1}{6}$[(a+5b)+(3a+2b)]×($\frac{4}{a+5b}$+$\frac{1}{3a+2b}$),利用基本不等式的性质,即可求得4a+7b的最小值.
解答 解:由$\frac{4}{a+5b}+\frac{1}{3a+2b}=6$,则4a+7b=$\frac{1}{6}$(4a+7b)×($\frac{4}{a+5b}$+$\frac{1}{3a+2b}$),
=$\frac{1}{6}$[(a+5b)+(3a+2b)]×($\frac{4}{a+5b}$+$\frac{1}{3a+2b}$),
=$\frac{1}{6}$(4+1+$\frac{a+5b}{3a+2b}$+$\frac{4(3a+2b)}{a+5b}$)≥$\frac{1}{6}$(5+2$\sqrt{\frac{a+5b}{3a+2b}×\frac{4(3a+2b)}{a+5b}}$)=$\frac{3}{2}$,
当且仅当$\frac{a+5b}{3a+2b}$=$\frac{4(3a+2b)}{a+5b}$,则a=$\frac{1}{26}$,b=$\frac{5}{26}$时取等号,
∴4a+7b的最小值$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查基本不等式的应用,考查转化思想,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15.侧面都是直角三角形的正三棱锥,底面边长为2,则此棱锥的全面积是( )
| A. | $3+\sqrt{3}$ | B. | $6+2\sqrt{3}$ | C. | $6+\sqrt{3}$ | D. | $3+2\sqrt{3}$ |
13.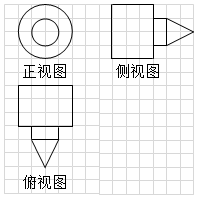 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(| A. | $(18+\sqrt{3})π$ | B. | $(21+\sqrt{3})π$ | C. | $(18+\sqrt{5})π$ | D. | $(21+\sqrt{5})π$ |
10.定义在R上的奇函数f(x)对任意x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$,若实数m,n满足f(m2+4m+12)+f(n2-6n)<0,则|m-2n-4|的取值范围为( )
| A. | $[\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1]$ | B. | $(\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1)$ | C. | $[12-\sqrt{5},12+\sqrt{5}]$ | D. | $(12-\sqrt{5},12+\sqrt{5})$ |
17.在等差数列{an}中,a3+a9=18-a6,Sn表示数列{an}的前n项和,则S11=( )
| A. | 66 | B. | 99 | C. | 198 | D. | 297 |
14.若$cos(α-\frac{π}{3})=\frac{2}{3}$,α是锐角,则sinα=( )
| A. | $\frac{{\sqrt{15}}}{6}$ | B. | $\frac{{\sqrt{5}-\sqrt{3}}}{6}$ | C. | $\frac{{2\sqrt{3}-\sqrt{5}}}{6}$ | D. | $\frac{{4-\sqrt{15}}}{6}$ |
15.在长为8cm的线段AB上任取一点C,作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小于15cm2的概率为( )
| A. | $\frac{8}{15}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |