题目内容
3．已知等差数列{an}，a11=103，a29=-53，求S39和a20．分析 根据等差数列的性质可得2a20=a11+a29，再根据前n项和公式计算即可．
解答 解：∵a11=103，a29=-53，
∴2a20=a11+a29=50，
∴a20=25，
∴S39=$\frac{39（{a}_{1}+{a}_{39}）}{2}$=39a20=39×25=1005
点评 本题考查等差数列的性质和前n项和公式，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
6．下列命题中：
①若a∈R，则（a+1）i是纯虚数；
②若a，b∈R且a＞b，则a+i3＞b+i2；
③若（x2-1）+（x2+3x+2）i是纯虚数，则实数x=±1；
④两个虚数不能比较大小．
其中，正确命题的序号是（ ）
①若a∈R，则（a+1）i是纯虚数；
②若a，b∈R且a＞b，则a+i3＞b+i2；
③若（x2-1）+（x2+3x+2）i是纯虚数，则实数x=±1；
④两个虚数不能比较大小．
其中，正确命题的序号是（ ）
| A． | ① | B． | ② | C． | ③ | D． | ④ |
15．侧面都是直角三角形的正三棱锥，底面边长为2，则此棱锥的全面积是（ ）
| A． | $3+\sqrt{3}$ | B． | $6+2\sqrt{3}$ | C． | $6+\sqrt{3}$ | D． | $3+2\sqrt{3}$ |
12．
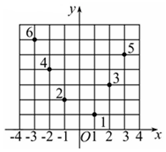如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横、纵坐标分别对应数列{an}（n∈N*）的前12项（即横坐标为奇数项，纵坐标为偶数项），按如此规律下去，则a2009+a2010+a2011等于（ ）
如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横、纵坐标分别对应数列{an}（n∈N*）的前12项（即横坐标为奇数项，纵坐标为偶数项），按如此规律下去，则a2009+a2010+a2011等于（ ）| A． | 2 011 | B． | 1 006 | C． | 1 005 | D． | 1 003 |
13．
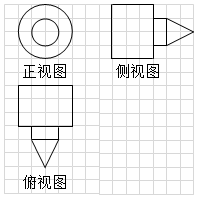放烟花是逢年过节一种传统庆祝节日的方式．已知一种烟花模型的三视图如图中的粗实线所示，网格纸上小正方形的边长为1，则该烟花模型的表面积为（
放烟花是逢年过节一种传统庆祝节日的方式．已知一种烟花模型的三视图如图中的粗实线所示，网格纸上小正方形的边长为1，则该烟花模型的表面积为（| A． | $（18+\sqrt{3}）π$ | B． | $（21+\sqrt{3}）π$ | C． | $（18+\sqrt{5}）π$ | D． | $（21+\sqrt{5}）π$ |