题目内容
数列{an}是等比数列,已知an>0,an=an+1+an+2,则数列的公比是 .
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:设等比数列{an}的公比为q,由题意可得q的一元二次方程,解方程可得.
解答:
解:设等比数列{an}的公比为q,由题意可得q>0,
∵an=an+1+an+2,∴an=anq+anq2,
∵an>0,∴1=q+q2,
解得q=
或q=
,
∵q>0,∴q=
故答案为:
∵an=an+1+an+2,∴an=anq+anq2,
∵an>0,∴1=q+q2,
解得q=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∵q>0,∴q=
-1+
| ||
| 2 |
故答案为:
-1+
| ||
| 2 |
点评:本题考查等比数列的通项公式,涉及一元二次方程的求解,属基础题.

练习册系列答案
相关题目
(1)若函数f(x)=2x2-ax-1在(0,1)内存在x0,使得f(x0)=0,求a的取值范围.
(2)方程mx2+2(m+3)x+2m+14=0有两相异实根,一个大于4,一个小于4,求m的取值范围.
(2)方程mx2+2(m+3)x+2m+14=0有两相异实根,一个大于4,一个小于4,求m的取值范围.
已知a,b,c,d是四条不重合的直线,其中c为a在平面α上的射影,d为b在平面α上的射影,则( )
| A、c∥d⇒a∥b |
| B、a⊥b⇒c⊥d |
| C、a∥b⇒c∥d |
| D、c⊥d⇒a⊥b |
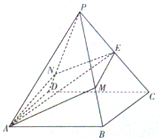 如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).
如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).