题目内容
已知函数f(x)=lnx-a(x-1),g(x)=ex.
(Ⅰ)若a=2,设h(x)=f(x+1)+g(x),当x≥0时,求h(x)的最小值;
(Ⅱ)过原点分别作函数f(x)与g(x)的切线,且两切线的斜率互为倒数,证明:a=0或1<a<2.
(Ⅰ)若a=2,设h(x)=f(x+1)+g(x),当x≥0时,求h(x)的最小值;
(Ⅱ)过原点分别作函数f(x)与g(x)的切线,且两切线的斜率互为倒数,证明:a=0或1<a<2.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,确定函数的单调性,即可求h(x)的最小值;
(Ⅱ)利用两切线的斜率互为倒数,可得
-a=
,从而可得ea-ae-1=0,令F(a)=ea-ae-1,确定其单调性,即可得出结论.
(Ⅱ)利用两切线的斜率互为倒数,可得
| 1 |
| x2 |
| lnx2-a(x2-1) |
| x2 |
解答:
(Ⅰ)解:h'(x)=ex+
-2,…(1分)
令p(x)=ex+
-2,
因为x≥0,
所以p′(x)=ex-
=
≥0,…(2分)
所以p(x),即h'(x))在[0,+∞)上递增,
所以h'(x)≥h'(0)=0,所以h(x)在[0,+∞)上递增,…(4分)
所以h(x)min=h(0)=1…(5分)
(2)证明:设g(x)的切点(x1,y1),f(x)的切点(x2,y2),
由
,解得
,…(7分)
所以
,
所以
-a=
,
所以lnx2=1-a,
所以x2=e1-a代入
-a=
得ea-ae-1=0,
令F(a)=ea-ae-1,则F'(a)=ea-e,
所以F(a)在(-∞,1)递减,在(1,+∞)上递增…(9分)
当a∈(-∞,1)时,因为F(0)=0,所以a=0…(10分)
当a∈(1,+∞)时,F(1)=-1<0,F(2)=e2-2e-1>0,所以1<a<2,
综上a=0或1<a<2…(12分)
| 1 |
| x+1 |
令p(x)=ex+
| 1 |
| x+1 |
因为x≥0,
所以p′(x)=ex-
| 1 |
| (x+1)2 |
| (x+1)2ex-1 |
| (x+1)2 |
所以p(x),即h'(x))在[0,+∞)上递增,
所以h'(x)≥h'(0)=0,所以h(x)在[0,+∞)上递增,…(4分)
所以h(x)min=h(0)=1…(5分)
(2)证明:设g(x)的切点(x1,y1),f(x)的切点(x2,y2),
由
|
|
所以
|
所以
| 1 |
| x2 |
| lnx2-a(x2-1) |
| x2 |
所以lnx2=1-a,
所以x2=e1-a代入
| 1 |
| x2 |
| 1 |
| e |
令F(a)=ea-ae-1,则F'(a)=ea-e,
所以F(a)在(-∞,1)递减,在(1,+∞)上递增…(9分)
当a∈(-∞,1)时,因为F(0)=0,所以a=0…(10分)
当a∈(1,+∞)时,F(1)=-1<0,F(2)=e2-2e-1>0,所以1<a<2,
综上a=0或1<a<2…(12分)
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查导数的几何意义,正确构建函数是关键.

练习册系列答案
相关题目
已知⊙C:x2+y2+2x-4y-4=0中弦AB的长为2
,则
•
=( )
| 3 |
| AB |
| AC |
| A、3 | ||
B、3
| ||
| C、6 | ||
D、6
|
下列几个式子化简后的结果是纯虚数的是( )
A、
| ||
| B、(1+i)3 | ||
| C、i4 | ||
D、
|
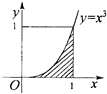 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1},向区域D内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域M={(x,y)|0≤x≤1,0≤y≤x3}的概率为
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1},向区域D内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域M={(x,y)|0≤x≤1,0≤y≤x3}的概率为