题目内容

已知函数f（x）=2sin2x-2sinxcos（x+
π
2
）．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）在区间[0，
π
2
]上的值域．
考点：三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：（1）利用二倍角的余弦公式及诱导公式化简，然后利用周期公式求周期；
（2）由x的范围求得2x的范围，由余弦函数的值域求得函数f（x）在区间[0，
π
2
]上的值域．
解答： 解：（1）f（x）=2sin2x-2sinxcos（x+
π
2
）
=2sin2x+2sinx•sinx=4sin2x=-2cos2x+2．
∴T=π；
（2）∵x∈[0，
π
2
]，
∴2x∈[0，π]，
则f（x）∈[0，4]．
函数f（x）在区间[0，
π
2
]上的值域为[0，4]．
点评：本题考查了三角函数中的恒等变换及应用，考查了三角函数的诱导公式及倍角公式，是中档题．
练习册系列答案
相关题目
下列几个式子化简后的结果是纯虚数的是（　　）
A、
1-i
i
B、（1+i）3
C、i4
D、
1-i
1+i
已知函数f（x）=ax+x2-xlna（a＞0且a≠1）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）a＞l，证明：当x∈（0，+∞）时，f（x）＞f（-x）；
（Ⅲ）若对任意x1，x2，x1≠x2，且当f（x1）=f（x2）时，有x1+x2＜0，求a的取值范围．
已知f（x）=sin（2x+
π
3
）+1，x∈R．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的单调增区间．
已知函数f（x）=lnx-
1
2
ax2+bx（a＞0），f′（1）=0．
（Ⅰ）试用含a的式子表示b，并求f（x）的单调区间；
（Ⅱ）若f（x）在（
1
2
，+∞）上有两个零点，求实数a的取值范围．
设函数f(x)=
x
ex
(e=2.71828…是自然对数的底数)．
（1）求f（x）的单调区间及最大值；
（2）?x∈（0，+∞），2|lnx-ln2|≥f（x）+c恒成立，试求实数c的取值范围．
抛物线3y2+2x=0的准线方程为
 
．
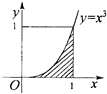如图，设区域D={（x，y）|0≤x≤1，0≤y≤1}，向区域D内随机投一点，且投入到区域内任一点都是等可能的，则点落入到阴影区域M={（x，y）|0≤x≤1，0≤y≤x3}的概率为
 
．
若直线y=kx与圆x2+（y-b）2=1的两个交点关于直线3x+y-6=0对称，则
b
k
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网