题目内容
设变量x、y满足约束条件
,其中k∈R,k>0,
(1)当k=1时,
的最大值为 ;
(2)若
的最大值为
,则实数k的取值范围是 .
|
(1)当k=1时,
| y-1 |
| x+1 |
(2)若
| y-1 |
| x+1 |
| 1 |
| 2 |
考点:简单线性规划
专题:不等式的解法及应用
分析:(1)作出不等式组对应的平面区域,利用数形结合即可得到结论,
(2)根据
的最大值为
,利用数形结合即可得到结论.
(2)根据
| y-1 |
| x+1 |
| 1 |
| 2 |
解答:
 解:(1)k=1时,作出不等式组对应的平面区域如图:
解:(1)k=1时,作出不等式组对应的平面区域如图:
设z=
,则z的几何意义为动点到定点P(-1,1)的斜率,
则由图象可知CP的斜率最大,
由
,得
,即C(2,2),
则z=
的最大值为
=
.
(2)若
的最大值为
,
即
=
,
则y-1=
(x+1),
由
,
解得
,即C(
,
)此时C也在直线y-1=k(x-1)上,
即
-1=k(
-1),
解得k=2.
故答案为:
,{2}
 解:(1)k=1时,作出不等式组对应的平面区域如图:
解:(1)k=1时,作出不等式组对应的平面区域如图:
设z=
| y-1 |
| x+1 |
则由图象可知CP的斜率最大,
由
|
|
则z=
| y-1 |
| x+1 |
| 2-1 |
| 2+1 |
| 1 |
| 3 |
(2)若
| y-1 |
| x+1 |
| 1 |
| 2 |
即
| y-1 |
| x+1 |
| 1 |
| 2 |
则y-1=
| 1 |
| 2 |
由
|
解得
|
| 5 |
| 3 |
| 7 |
| 3 |
即
| 7 |
| 3 |
| 5 |
| 3 |
解得k=2.
故答案为:
| 1 |
| 3 |
点评:本题主要考查线性规划的应用,利用z的几何意义,以及直线的斜率公式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
直线x-y+1=0与圆x2+(y+1)2=2的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、不能确定 |
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a8+b8=( )
| A、28 | B、47 | C、76 | D、123 |
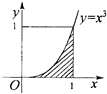 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1},向区域D内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域M={(x,y)|0≤x≤1,0≤y≤x3}的概率为
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1},向区域D内随机投一点,且投入到区域内任一点都是等可能的,则点落入到阴影区域M={(x,y)|0≤x≤1,0≤y≤x3}的概率为