题目内容
已知某几何体的直观图和三视图如图所示,其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
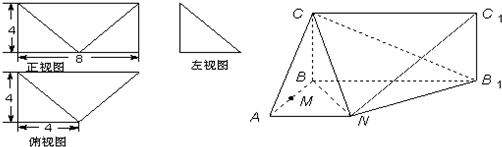
(1)证明:面BCN⊥面C1NB1
(2)求平面CNB1与平面C1NB1所成角的余弦值.

(1)证明:面BCN⊥面C1NB1
(2)求平面CNB1与平面C1NB1所成角的余弦值.
考点:与二面角有关的立体几何综合题,由三视图求面积、体积
专题:空间位置关系与距离,空间角
分析:(Ⅰ)根据题意,可得BA,BC,BB1两两垂直,以BA,BB1,BC分别为x,y,z轴建立空间直角坐标系,用坐标表示点、向量,利用数量积证明NB⊥NB1,BN⊥B1C1,即可证明BN⊥平面C1NB1.
(Ⅱ)求出平面C1B1N、平面NCB1的一个法向量,利用向量的夹角公式,可求二面角C-NB1-C1的余弦值.
(Ⅱ)求出平面C1B1N、平面NCB1的一个法向量,利用向量的夹角公式,可求二面角C-NB1-C1的余弦值.
解答:
(1)证明:∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形,
∴BA,BC,BB1两两垂直.
以BA,BB1,BC分别为x,y,z轴建立空间直角坐标系如图.--------------(2分)

则B(0,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4).
∴
•
=-16+16+0=0,
•
=(4,4,0)•(0,0,4)=0------------(4分)
∴NB⊥NB1,BN⊥B1C1.
又NB1与B1C1相交于B1,∴BN⊥平面C1NB1.-------------------(6分)
(2)解:∵BN⊥平面C1NB1,∴
是平面C1B1N的一个法向量
=(4,4,0),------------(8分)
设
=(x,y,z)为平面NCB1的一个法向量,则
∴可取
=(1,1,2).------------(10分)
∴cos<
,
>=
=
∴所求二面角C-NB1-C1的余弦值为
.------------(12分)
∴BA,BC,BB1两两垂直.
以BA,BB1,BC分别为x,y,z轴建立空间直角坐标系如图.--------------(2分)

则B(0,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4).
∴
| BN |
| NB1 |
| BN |
| B1C1 |
∴NB⊥NB1,BN⊥B1C1.
又NB1与B1C1相交于B1,∴BN⊥平面C1NB1.-------------------(6分)
(2)解:∵BN⊥平面C1NB1,∴
| BN |
| n1 |
设
| n2 |
|
∴可取
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 3 |
∴所求二面角C-NB1-C1的余弦值为
| ||
| 3 |
点评:本题考查线面垂直,考查面面角,解题的关键是构建空间直角坐标系,确定平面的法向量.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
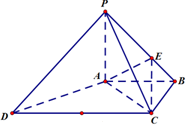 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC= 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形且∠A1AC=∠DAB=60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形且∠A1AC=∠DAB=60°,平面AA1C1C⊥平面ABCD.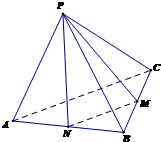 (文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示).
(文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示). 如图,在四棱锥S-ABCD中,底面ABCD是正方形,四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.