题目内容
如图，在四棱锥S-ABCD中，底面ABCD是正方形，四个侧面都是等边三角形，AC与BD的交点为O，E为侧棱SC的中点．（1）求证：平面SA∥平面BDE；
（2）平面BDE⊥平面SAC；
（3）求二面角S-AB-C的余弦值．
考点：与二面角有关的立体几何综合题,平面与平面平行的判定,平面与平面垂直的判定
专题：综合题,空间位置关系与距离,空间角
分析：（1）连接OE，利用OE为△SAC的中位线，可得SA∥OE，由此能够证明SA∥平面BDE；
（2）先证明BD⊥SO，再证明BD⊥AC，根据线面垂直的判定定理，可得BD⊥平面SAC，由此能够证明平面BDE⊥平面SAC；
（3）取AB的中点F，连接SF，OF，则SF⊥AB，OF⊥AB，所以∠SFO为二面角S-AB-C的平面角，利用余弦函数，可求二面角S-AB-C的余弦值．
（2）先证明BD⊥SO，再证明BD⊥AC，根据线面垂直的判定定理，可得BD⊥平面SAC，由此能够证明平面BDE⊥平面SAC；
（3）取AB的中点F，连接SF，OF，则SF⊥AB，OF⊥AB，所以∠SFO为二面角S-AB-C的平面角，利用余弦函数，可求二面角S-AB-C的余弦值．
解答：
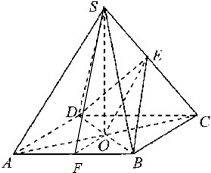（1）证明：连接OE，
因为E为侧棱SC的中点时，OE为△SAC的中位线，
所以SA∥OE，
因为SA?平面BDE，OE?平面BDE，
所以SA∥平面BDE；
（2）证明：因为SB=SD，O是BD中点，
所以BD⊥SO，
又因为四边形ABCD是正方形，所以BD⊥AC，
因为AC∩SO=O，所以BD⊥平面SAC，
又因为BD?平面BDE，
所以平面BDE⊥平面SAC；
（3）解：取AB的中点F，连接SF，OF，则SF⊥AB，OF⊥AB，
所以∠SFO为二面角S-AB-C的平面角，
设AB=2a，则SF=
a，OF=a，
所以cos∠SFO=
=
．
（1）证明：连接OE，因为E为侧棱SC的中点时，OE为△SAC的中位线，
所以SA∥OE，
因为SA?平面BDE，OE?平面BDE，
所以SA∥平面BDE；
（2）证明：因为SB=SD，O是BD中点，
所以BD⊥SO，
又因为四边形ABCD是正方形，所以BD⊥AC，
因为AC∩SO=O，所以BD⊥平面SAC，
又因为BD?平面BDE，
所以平面BDE⊥平面SAC；
（3）解：取AB的中点F，连接SF，OF，则SF⊥AB，OF⊥AB，
所以∠SFO为二面角S-AB-C的平面角，
设AB=2a，则SF=
| 3 |
所以cos∠SFO=
| OF |
| SF |
| ||
| 3 |
点评：本题主要考查空间直线和平面平行以及面面垂直的判定，考查面面角，要求熟练掌握相应的判定定理．
练习册系列答案
相关题目
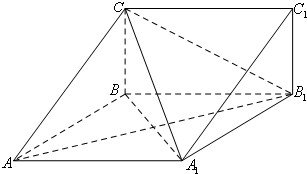如图，在三棱柱ABC-A1B1C1中，四边形A1ABB1为菱形，∠A1AB=45°，四边形BCC1B1为矩形，若AC=5，AB=4，BC=3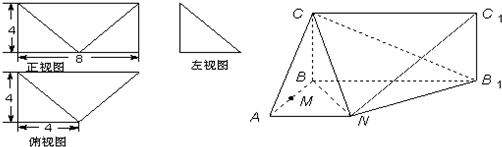
在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠ABC=60°，AB=2CB=2．在梯形ACEF中，EF∥AC，且AC=2EF，EC⊥平面ABCD．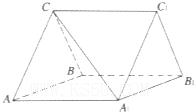
如图，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．
如图，正三棱柱ABC-A′B′C′中，D是BC的中点，AA′=AB=2