题目内容
不等式(k-1)x2-2(k-1)x+3(k+1)>0对于任何x∈R都成立,则k∈ .
考点:函数恒成立问题
专题:不等式的解法及应用
分析:分二次项系数为0和不为0讨论,当二次项系数不为0时,只需二次项系数大于0,且判别式小于0联立不等式组求解k的取值范围即可.
解答:
解:当k=1时,不等式化为3×(1+1)=6>0恒成立;
当k≠1时,要使不等式(k-1)x2-2(k-1)x+3(k+1)>0对于任何x∈R都成立,
则
,即
.
解得:k>1.
综上,k的范围是[1,+∞).
故答案为:[1,+∞).
当k≠1时,要使不等式(k-1)x2-2(k-1)x+3(k+1)>0对于任何x∈R都成立,
则
|
|
解得:k>1.
综上,k的范围是[1,+∞).
故答案为:[1,+∞).
点评:本题考查恒成立问题,考查了分类讨论的数学思想方法,解答的关键是把不等式恒成立转化为不等式对应的函数的图象与x轴没有交点,是中档题.

练习册系列答案
相关题目
“|x-1|<2”是“(x-1)(x-3)<0”成立的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
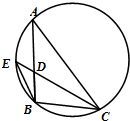 如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=
如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=