题目内容

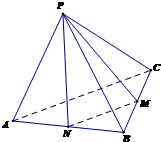（文科）如图，正四面体P-ABC中，M为线段BC的中点，求异面直线PM与AC所成的角（结果用反三角函数值表示）．
考点：异面直线及其所成的角
专题：转化思想,空间位置关系与距离,空间角
分析：取线段AB的中点N，连接MN、PN，M、N分别为线段BC、AB的中点，判断∠PMN为异面直线PM与AC所成的角（或其补角），通过解△PMN，求出结果即可．
解答： 解：取线段AB的中点N，连接MN、PN，M、N分别为线段BC、AB的中点
则MN∥AC，
所以∠PMN为异面直线PM与AC所成的角（或其补角）   5分
设正四面体P-ABC的棱长为a
等边三角形PBC中，M为BC的中点，PM=
PB2-BM2
=
3
2
a
等边三角形PBA中，N为BA的中点，PN=
PB2-BN2
=
3
2
aMN=
1
2
AC=
1
2
a     8分
三角形PMN中，cos∠PMN=
PM2+MN2-PN2
2PM•MN
=
(
3
2
a)2+(
a
2
)2-(
3
2
a)2
2(
3
2
a)(
a
2
)
=
3
6
   10分
得∠PMN=arccos
3
6
，
故异面直线PM与AC所成的角为arccos
3
6
    12分．
点评：本题考查求异面直线角，用好异面直线所成角的对应是解题的关键，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
在△ABC中，已知|BC|=2，且
|AB|
|AC|
=
2
，求点A的轨迹方程，并说明轨迹是什么图形．
已知不等式x2-2ax+2＞0在x∈（-1，2）上恒成立，求实数a的取值范围．
已知某几何体的直观图和三视图如图所示，其正视图为矩形，左视图为等腰直角三角形，俯视图为直角梯形．

（1）证明：面BCN⊥面C1NB1
（2）求平面CNB1与平面C1NB1所成角的余弦值．
已知向量
m
=（sin（2x+
π
6
），sinx），
n
=（1，sinx），f（x）=
m
•
n
-
1
2
．
（Ⅰ）求函数f（x）的单调递减区间；
（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，a=2
3
，f(
A
2
)=
1
2
，若
3
sin（A+C）=2cosC，求b的大小．
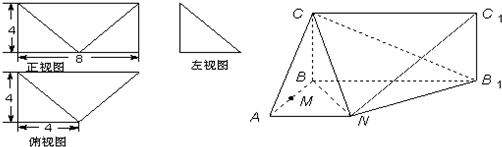
在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠ABC=60°，AB=2CB=2．在梯形ACEF中，EF∥AC，且AC=2EF，EC⊥平面ABCD．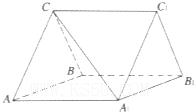
（Ⅰ）求证：BC⊥AF；
（Ⅱ）若二面角D-AF-C为45°，求CE的长．
如图，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．
（Ⅰ）证明：AB⊥A1C；
（Ⅱ）若AB=CB=2，A1C=
6
，求二面角B-AC=A1的余弦值．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点为F1(-
2
，0)，短轴的端点到右焦点的距离为
3
．
（1）求椭圆C的方程；
（2）若直线l与圆4x2+4y2=3相切，且与椭圆C交于A，B两点，求|AB|的最大值．
已知函数f（x）对于一切实数x，y均有f（x+y）-f（y）=x（x+2y+1）成立，且f（1）=0，则当x∈（0，
1
2
），不等式f（x）+2＜logax恒成立时，实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网