题目内容
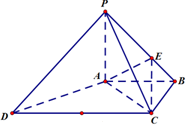 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=| 1 |
| 2 |
| 1 |
| 2 |
(1)求证:PD∥平面AEC.
(2)求二面角A-CE-P的余弦值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)由已知条件,推导出EM∥PD,利用直线与平面平行的判定定理能证明PD∥面EAC.
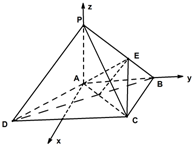
(2)以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,求出平面EAC的一个法向量,平面PBC的一个法向量,利用向量的夹角公式,即可得出结论.
(2)以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,求出平面EAC的一个法向量,平面PBC的一个法向量,利用向量的夹角公式,即可得出结论.
解答:
 (1)证明:连结BD,交AC于点M,连结EM,
(1)证明:连结BD,交AC于点M,连结EM,
∵AB∥DC,AB=
CD,
∴
=
=
…(1分)
又∵
=
,∴
=
…(2分)
∴在△BPD中,EM∥PD.
∵PD不包含于平面EAC,EM?平面EAC
∴PD∥面EAC …(5分)
(2)解:由已知可以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,
设PA=AB=BC=a,则A(0,0,0),C(a,a,0),B(0,a,0),P(0,0,a),E(0,
,
)
设
=(x,y,1)为平面EAC的一个法向量,
则
,
解得x=
,y=-
,∴
=(
,-
,1). …(9分)
同理可得平面PBC的一个法向量
=(0,1,1)…(11分)
∴cos<
,
>=
=
…(13分)
∴二面角A-CE-P的余弦值为
. …(14分)
 (1)证明:连结BD,交AC于点M,连结EM,
(1)证明:连结BD,交AC于点M,连结EM,∵AB∥DC,AB=
| 1 |
| 2 |
∴
| BM |
| MD |
| AB |
| CD |
| 1 |
| 2 |
又∵
| BE |
| PE |
| 1 |
| 2 |
| BM |
| MD |
| BE |
| PE |
∴在△BPD中,EM∥PD.
∵PD不包含于平面EAC,EM?平面EAC
∴PD∥面EAC …(5分)
(2)解:由已知可以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,
设PA=AB=BC=a,则A(0,0,0),C(a,a,0),B(0,a,0),P(0,0,a),E(0,
| 2a |
| 3 |
| a |
| 3 |

设
| n1 |
则
|
解得x=
| 1 |
| 2 |
| 1 |
| 2 |
| n1 |
| 1 |
| 2 |
| 1 |
| 2 |
同理可得平面PBC的一个法向量
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 6 |
∴二面角A-CE-P的余弦值为
| ||
| 6 |
点评:本题考查直线与平面平行的证明,考查平面与平面所成角的应用,解题时要注意等价转化思想和向量法的合理运用.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 如图,PA,PB是圆O的两条切线,A,B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且∠DAQ=∠PBC.求证:
如图,PA,PB是圆O的两条切线,A,B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且∠DAQ=∠PBC.求证: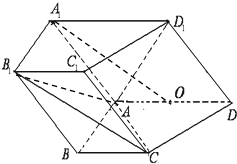 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=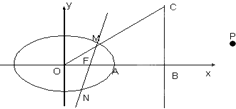 已知椭圆
已知椭圆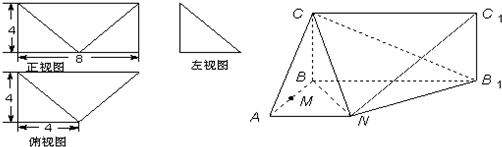
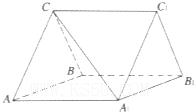 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.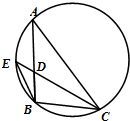 如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=
如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=