题目内容
已知点A(1,0),直线l:y=2x-6,点R是直线l上的一点,动点P满足
=2
.
(1)求动点P的轨迹方程;
(2)动点P在运动过程中是否经过圆x2+y2+4x+3=0?请说明理由.
| RA |
| AP |
(1)求动点P的轨迹方程;
(2)动点P在运动过程中是否经过圆x2+y2+4x+3=0?请说明理由.
考点:轨迹方程,点与圆的位置关系
专题:综合题,直线与圆
分析:(1)设P(x,y)是轨迹上任意一点,对应的直线l上的点为R(x0,y0),利用动点P满足
=2
,确定坐标之间的关系,根据R(x0,y0)在直线l上,可得动点P的轨迹方程;
(2)求出C(-2,0)到直线2x-y=0的距离,确定P在圆外,即可得出结论.
| RA |
| AP |
(2)求出C(-2,0)到直线2x-y=0的距离,确定P在圆外,即可得出结论.
解答:
解:(1)设P(x,y)是轨迹上任意一点,对应的直线l上的点为R(x0,y0),则
=(1-x0,-y0),
=(x-1,y),
由
=2
,得
,即
,
因为R(x0,y0)在直线l上,
所以-2y=2(3-2x)-6,即2x-y=0;
(2)圆x2+y2+4x+3=0即(x+2)2+y2=1,其圆心为C(-2,0),半径r=1,
C(-2,0)到直线2x-y=0的距离d=
=
>1=r,
所以动点P在运动过程中不经过圆x2+y2+4x+3=0.
| RA |
| AP |
由
| RA |
| AP |
|
|
因为R(x0,y0)在直线l上,
所以-2y=2(3-2x)-6,即2x-y=0;
(2)圆x2+y2+4x+3=0即(x+2)2+y2=1,其圆心为C(-2,0),半径r=1,
C(-2,0)到直线2x-y=0的距离d=
| |2×(-2)| | ||
|
| 4 | ||
|
所以动点P在运动过程中不经过圆x2+y2+4x+3=0.
点评:本题考查代入法求轨迹方程,考查直线与圆的位置关系,确定P的轨迹方程是关键.

练习册系列答案
相关题目
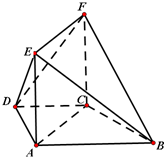 如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.
如图,在梯形ABCD中,AB∥CD,∠ABC=60°,AD=CD=CB=a,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a.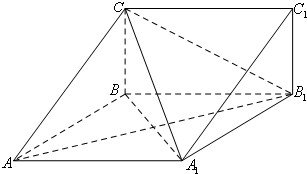 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3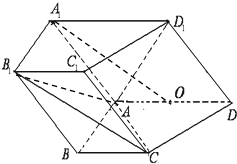 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=