题目内容
20．椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的离心率是（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
分析 根据题意，由椭圆的标准方程可得a=2，b=$\sqrt{2}$，由c2=a2-b2计算可得c的值，由离心率计算公式e=$\frac{c}{a}$计算可得答案．
解答 解：根据题意，椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1，
其中a=2，b=$\sqrt{2}$，
则c2=a2-b2=2，即c=$\sqrt{2}$；
故其离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$；
故选：A．
点评 本题考查椭圆的基本性质，关键是正确运算离心率的计算公式，注意该椭圆的焦点在y轴上．
练习册系列答案
相关题目
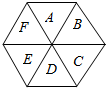如图，一个正六边形分为6个区域A、B、C、D、E、F，现给这6个区域着色，要求同一区域染同一种颜色，相邻的两个区域不得使用同一颜色，现有红，黄，蓝，绿四种颜色可供选择，且A必须涂红色，则有多少种不同的着色方法？