题目内容
10.已知函数f(x)=logax(a>0且a≠1)(1)当a=3时,求方程f($\frac{27}{x}$)f(3x)=-5的解;
(2)若f(3a-1)>f(a),求实数a的取值范围;
(3)当a=$\frac{1}{2}$时,设g(x)=f(x)-3x+4,求证:对任意λ>0,都存在μ>0,使得g(x)<0对x∈(λμ,+∞)恒成立.
分析 (1)当a=3时,f(x)=log3x,f($\frac{27}{x}$)f(3x)=(log327-log3x)(log33+log3x)=(3-log3x)(1+log3x)=-5,解得答案;
(2)分讨论满足不等式f(3a-1)>f(a)=1的a的范围,综合讨论结果,可得答案;
(3)当a=$\frac{1}{2}$时,g(x)=${log}_{\frac{1}{2}}x$-3x+4为减函数,且g(x)<0对x∈(2,+∞)恒成立.进而得到答案.
解答 解:(1)当a=3时,f(x)=log3x,
∴f($\frac{27}{x}$)f(3x)=(log327-log3x)(log33+log3x)=(3-log3x)(1+log3x)=-5,
解得:log3x=4,或log3x=-2,
解得:x=81,或x=$\frac{1}{9}$;
(2)∵f(3a-1)>f(a)=1,
①当0<a<1时,0<3a-1<a,解得:0<a<$\frac{1}{2}$,
②当a>1时,3a-1>a,解得:a>1,
综上可得:0<a<$\frac{1}{2}$,或a>1;
证明:(3)当a=$\frac{1}{2}$时,g(x)=f(x)-3x+4=${log}_{\frac{1}{2}}x$-3x+4为减函数,
由g(2)=-1-9+4=-6<0,
故g(x)<0对x∈(2,+∞)恒成立.
故对任意λ>0,都存在μ=$\frac{2}{λ}$>0,使得λμ=2,
即对任意λ>0,都存在μ>0,使得g(x)<0对x∈(λμ,+∞)恒成立.
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
5.sinx=$\frac{1}{2}$,则sin($\frac{π}{2}$+x)•tan(π-x)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
15.下列命题正确的是( )
| A. | y=sinx在[0,π]内是单调函数 | |
| B. | 在第二象限内,y=sinx是减函数,y=cosx也是减函数 | |
| C. | y=cosx的增区间是[0,π] | |
| D. | y=sinx在区间[$\frac{π}{2}$,π]上是减函数 |
20.椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的离心率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
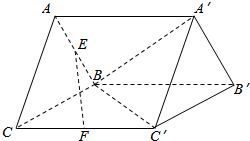 如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.