题目内容
8.设数列{an}满足an+1=$\frac{4{a}_{n}-1}{{a}_{n}+2}$,当首项a1=$\frac{7}{10}$时,此数列只有10项.分析 把已知数列递推式变形,得到${a}_{n}=\frac{9}{4-{a}_{n+1}}-2$.由数列{an}只有10项,可得a10=-2.依次由变形后的递推式求得首项得答案.
解答 解:由an+1=$\frac{4{a}_{n}-1}{{a}_{n}+2}$=$\frac{4({a}_{n}+2)-9}{{a}_{n}+2}$=$4-\frac{9}{{a}_{n}+2}$,得
${a}_{n}=\frac{9}{4-{a}_{n+1}}-2$.
若数列{an}只有10项,则a10=-2.
∴${a}_{9}=\frac{9}{6}-2=-\frac{1}{2}$,${a}_{8}=\frac{9}{\frac{9}{2}}-2=0$,${a}_{7}=\frac{9}{4}-2=\frac{1}{4}$,
${a}_{6}=\frac{9}{\frac{15}{4}}-2=\frac{2}{5}$,${a}_{5}=\frac{9}{\frac{18}{5}}-2=\frac{1}{2}$,${a}_{4}=\frac{9}{\frac{7}{2}}-2=\frac{4}{7}$,
${a}_{3}=\frac{9}{\frac{24}{7}}-2=\frac{5}{8}$,${a}_{2}=\frac{9}{\frac{27}{8}}-2=\frac{2}{3}$,${a}_{1}=\frac{9}{\frac{10}{3}}-2=\frac{7}{10}$.
故答案为:$\frac{7}{10}$.
点评 本题考查数列递推式,考查计算能力,对题意的理解是解答该题的关键,是中档题.

练习册系列答案
相关题目
20.椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的离心率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
13.已知f(x),g(x),h(x)为R上的函数,其中函数f(x)为奇函数,函数g(x)为偶函数,则( )
| A. | 函数h(g(x))为偶函数 | B. | 函数h(f(x))为奇函数 | C. | 函数g(h(x))为偶函数 | D. | 函数f(h(x))为奇函数 |
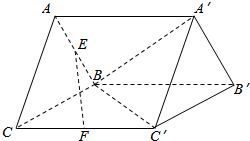 如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.