题目内容
9.f(x)=ax2+bx+1在[3-a,5]上是偶函数,则f(x)在[3-a,5]的最小值为1.分析 根据偶函数的定义域关于原点对称,可得a值,进而根据二次函数的图象和性质,可得答案.
解答 解:函数f(x)=ax2+bx+1是定义在[3-a,5]上的偶函数,
可得b=0,并且3-a+5=0,解得a=8,
所以函数为:f(x)=8x2+1,x∈[-8,8],
函数在x=0时,取最小值为:1.
故答案为:1
点评 本题考查的知识点是函数奇偶性的性质,熟练掌握函数奇偶的定义是解答的关键,难度中档.

练习册系列答案
相关题目
20.椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的离心率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
4. 为了调查一款项链的销售数量x(件)与销售利润y(万元)之间的相关关系,某公司的市场专员作出调查并将结果统计如表所示:
为了调查一款项链的销售数量x(件)与销售利润y(万元)之间的相关关系,某公司的市场专员作出调查并将结果统计如表所示:
(Ⅰ)请在下列坐标纸中作出x,y的散点图;
(Ⅱ)若某同学根据如表中的数据(6,6)和(8,7)求得的直线方程为y=b′x+a′,请根据上表数据计算x,y的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并比较$\widehat{b}$与b′以及$\widehat{a}$与a′的大小关系.
(注,$\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\underset{\stackrel{n}{∑}}{i=1}x}_{i}^{2}-n\overline{{x}^{2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
 为了调查一款项链的销售数量x(件)与销售利润y(万元)之间的相关关系,某公司的市场专员作出调查并将结果统计如表所示:
为了调查一款项链的销售数量x(件)与销售利润y(万元)之间的相关关系,某公司的市场专员作出调查并将结果统计如表所示:| x(件) | 3 | 4 | 5 | 6 | 8 | 10 |
| y(万元) | 3 | 2 | 4 | 6 | 7 | 8 |
(Ⅱ)若某同学根据如表中的数据(6,6)和(8,7)求得的直线方程为y=b′x+a′,请根据上表数据计算x,y的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并比较$\widehat{b}$与b′以及$\widehat{a}$与a′的大小关系.
(注,$\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\underset{\stackrel{n}{∑}}{i=1}x}_{i}^{2}-n\overline{{x}^{2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
13.已知f(x),g(x),h(x)为R上的函数,其中函数f(x)为奇函数,函数g(x)为偶函数,则( )
| A. | 函数h(g(x))为偶函数 | B. | 函数h(f(x))为奇函数 | C. | 函数g(h(x))为偶函数 | D. | 函数f(h(x))为奇函数 |
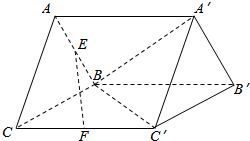 如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
如图,三棱柱ABC-A′B′C′,BC=1,BC′=1,CC′=$\sqrt{2}$,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.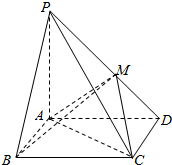 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.