题目内容
5.已知f(x)是定义在R上的奇函数,f(x+1)是偶函数,当x∈(2,4)时,f(x)=|x-3|,则f(1)+f(2)+f(3)+f(4)=( )| A. | 1 | B. | 0 | C. | 2 | D. | -2 |
分析 根据已知可得f(-x)=-f(x),f(-x+1)=f(x+1),结合x∈(2,4)时,f(x)=|x-3|,分别求出f(1),f(2),f(3),f(4)可得答案.
解答 解:∵f(x)是定义在R上的奇函数,f(x+1)是偶函数,
∴f(0)=0,f(-x)=-f(x),f(-x+1)=f(x+1),
∴f(x+4)=f[(x+3)+1]=f[-(x+3)+1]=f(-x-2)=-f(x+2)
=-f[(x+1)+1]=-f[-(x+1)+1]=-f(-x)=f(x),
∴函数f(x)是周期为4的周期函数,f(4)=f(0)=0,
∵当x∈(2,4)时,f(x)=|x-3|,
∴f(3)=0,f(4)=0,
f(1)=-f(-1)=-f(3)=0,
f(2)=-f(-2)=-f(2)=0,
故f(1)+f(2)+f(3)+f(4)=0,
故选:B
点评 本题考查的知识点是函数的奇偶性,函数求值,难度不大,属于基础题目.

练习册系列答案
相关题目
20.椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的离心率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
13.已知f(x),g(x),h(x)为R上的函数,其中函数f(x)为奇函数,函数g(x)为偶函数,则( )
| A. | 函数h(g(x))为偶函数 | B. | 函数h(f(x))为奇函数 | C. | 函数g(h(x))为偶函数 | D. | 函数f(h(x))为奇函数 |
20.已知函数f(x)为奇函数,且当x>0时,f(x)=x2+x,则f(-2)等于( )
| A. | -2 | B. | 2 | C. | -4 | D. | -6 |
15.若向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(1,-3),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
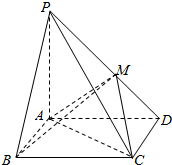 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.