题目内容
12．
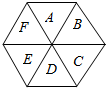如图，一个正六边形分为6个区域A、B、C、D、E、F，现给这6个区域着色，要求同一区域染同一种颜色，相邻的两个区域不得使用同一颜色，现有红，黄，蓝，绿四种颜色可供选择，且A必须涂红色，则有多少种不同的着色方法？
分析 分三类讨论：A、C、E用同一颜色、A、C、E用2种颜色、A、C、E用3种颜色，利用分步计数原理，可得结论．
解答 解：考虑A、C、E用同一颜色，此时共有1×3×3×3=27种方法．
考虑A、C、E用2种颜色，此时共有3×1×2×2×2=24种方法．
考虑A、C、E用3种颜色，此时共有A32×2×2×2=48种方法．
故总计有27+24+48=99种方法．
点评 本题考查理解题意能力，考查分类思想的运用，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
20．椭圆$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{4}$=1的离心率是（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
7．已知集合P={x|6＜x＜8}，Q={x|x∈N}，则P∩Q等于（ ）
| A． | {7} | B． | {6，7} | C． | {6，7，8} | D． | {x|6＜x＜8} |
4．
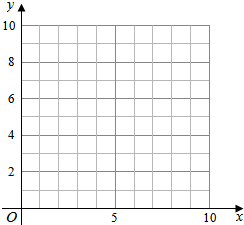为了调查一款项链的销售数量x（件）与销售利润y（万元）之间的相关关系，某公司的市场专员作出调查并将结果统计如表所示：
（Ⅰ）请在下列坐标纸中作出x，y的散点图；
（Ⅱ）若某同学根据如表中的数据（6，6）和（8，7）求得的直线方程为y=b′x+a′，请根据上表数据计算x，y的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，并比较$\widehat{b}$与b′以及$\widehat{a}$与a′的大小关系．
（注，$\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\underset{\stackrel{n}{∑}}{i=1}x}_{i}^{2}-n\overline{{x}^{2}}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）
为了调查一款项链的销售数量x（件）与销售利润y（万元）之间的相关关系，某公司的市场专员作出调查并将结果统计如表所示：| x（件） | 3 | 4 | 5 | 6 | 8 | 10 |
| y（万元） | 3 | 2 | 4 | 6 | 7 | 8 |
（Ⅱ）若某同学根据如表中的数据（6，6）和（8，7）求得的直线方程为y=b′x+a′，请根据上表数据计算x，y的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，并比较$\widehat{b}$与b′以及$\widehat{a}$与a′的大小关系．
（注，$\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\underset{\stackrel{n}{∑}}{i=1}x}_{i}^{2}-n\overline{{x}^{2}}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）