题目内容
3.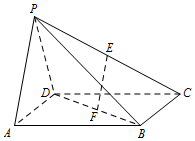 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.(Ⅰ)求证:EF||平面PAD;
(Ⅱ)求三棱锥P-CDF的体积.
分析 (Ⅰ)连接AC,AC∩BD=F,EF∥PA,由此能证明EF∥平面PAD.
(Ⅱ)法一:取AD中点O,连接OP,OF,推导出OP⊥平面ABCD,三棱锥P-CDF的体积${V}_{P-CDF}=\frac{1}{3}{S}_{△CDF}•OP$.
法二:三棱锥P-CDF的体积VP-CDF=VF-PCD,由此能求出结果.
解答 证明:(Ⅰ)连接AC,AC∩BD=F,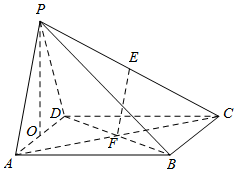
在△PAC中,EF∥PA.…(3分)
又PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD.…(6分)
解:(Ⅱ)解法一:取AD中点O,连接OP,OF,
∵PA=PD,∴OP⊥AD.
又侧面PAD⊥底面ABCD,且侧面PAD∩底面ABCD=AD,
∴OP⊥平面ABCD.…(9分)
∴三棱锥P-CDF的体积${V}_{P-CDF}=\frac{1}{3}{S}_{△CDF}•OP$=$\frac{1}{3}×\frac{1}{2}×2×1×1$=$\frac{1}{3}$.…(12分)
解法二:∵侧面PAD⊥底面ABCD,
且侧面PAD∩底面ABCD=AD,AD⊥CD,
∴CD⊥平面PAD.
∴CD⊥PA,CD⊥PD.
又PA⊥PD,且CD∩PD=D,∴PA⊥平面PCD,故EF⊥平面PCD,…(9分)
∵PD=$\sqrt{2}$,EF=$\frac{1}{2}$PA=$\frac{\sqrt{2}}{2}$,
∴三棱锥P-CDF的体积:
VP-CDF=VF-PCD=$\frac{1}{3}{S}_{△PCD}•EF$=$\frac{1}{3}×\frac{1}{2}×2×\sqrt{2}×\frac{\sqrt{2}}{2}$=$\frac{1}{3}$.…(12分)
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、转化化归思想,考查数据处理能力和运用意识,是中档题.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | -1 |
其中直径在区间(148,152]内的零件为一等品.
| 编号 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 |
| 直径 | 151 | 148 | 149 | 151 | 149 | 152 | 147 | 146 | 153 | 148 |
(2)从一等品零件中,随机抽取2个.用ξ表示这2个零件直径之差的绝对值,求随机变量ξ的分布列及数学期望.
| A. | y′=x2cosx-2xsin x | B. | y′=2xcos x+x2sin x | ||
| C. | y′=2xcosx-x2sinx | D. | y′=xcosx-x2sin x |
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |