题目内容
14.有编号为D1,D2,…,D10的10个零件,测量其直径(单位:mm),得到下面数据:其中直径在区间(148,152]内的零件为一等品.
| 编号 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 |
| 直径 | 151 | 148 | 149 | 151 | 149 | 152 | 147 | 146 | 153 | 148 |
(2)从一等品零件中,随机抽取2个.用ξ表示这2个零件直径之差的绝对值,求随机变量ξ的分布列及数学期望.
分析 (1)由所给数据可知,10个零件中一等品零件共有5个.从上述10个零件中,随机抽取2个,基本事件总数n=${C}_{10}^{2}$,2个零件均为一等品包含的基本事件个数m=${C}_{5}^{2}$,由此能求出这2个零件均为一等品的概率.
(2)ξ的可能取值为:0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和数学期望Eξ.
解答 (本题满分12分)
解:(1)由所给数据可知,10个零件中一等品零件共有5个.(1分)
设“从上述10个零件中,随机抽取2个,2个零件均为一等品”为事件A,
则$P(A)=\frac{C_5^2}{{C_{10}^2}}=\frac{2}{9}$.(4分)
(2)∵ξ的可能取值为:0,1,2,3,(5分)
且$P(ξ=0)=\frac{2}{C_5^2}=\frac{1}{5}$,
$P(ξ=1)=\frac{2}{C_5^2}=\frac{1}{5}$,
$P(ξ=2)=\frac{4}{C_5^2}=\frac{2}{5}$,
$P(ξ=3)=\frac{2}{C_5^2}=\frac{1}{5}$--(9分)
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P(ξ) | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{2}{5}$ | $\frac{1}{5}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,考查推理论证能力、运算求解能力,考查整体思想、转化化归思想,考查数据处理能力和运用意识,是中档题.

练习册系列答案
相关题目
2.已知函数f(x)=e|x|+x2,若实数a满足f(log2a)≤f(1),则a的取值范围是( )
| A. | (0,1] | B. | [$\frac{1}{2}$,2] | C. | (0,2] | D. | [2,+∞) |
19.已知f (x)是可导的函数,且f′(x)<f(x)对于x∈R恒成立,则( )
| A. | f(1)<ef(0),f(2016)>e2016f(0) | B. | f(1)>ef(0),f(2016)>e2016f(0) | ||
| C. | f(1)>ef(0),f(2016)<e2016f(0) | D. | f(1)<ef(0),f(2016)<e2016f(0) |
6.在△ABC中,A:B:C=1:2:3,则a:b:c=( )
| A. | 1:2:3 | B. | sin1:sin2:sin3 | C. | 1:$\sqrt{3}$:2 | D. | 1:2:$\sqrt{3}$ |
 如图,D是直角△ABC斜边BC上一点,$AC=\sqrt{2}DC$.
如图,D是直角△ABC斜边BC上一点,$AC=\sqrt{2}DC$.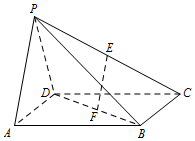 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.