题目内容
15.设命题p:实数a满足不等式3a≤9,命题q:x2+3(3-a)x+9≥0的解集为R.已知“p∧q”为真命题,并记为条件r,且条件t:实数a满足a<m或$a>m+\frac{1}{2}$.(1)求条件r的等价条件(用a的取值范围表示);
(2)若r是¬t的必要不充分条件,求正整数m的值.
分析 (1)求出“p∧q”为真命题,实数a的取值范围
(2)结合r是¬t的必要不充分条件,可得满足条件的正整数m的值.
解答 解:(1)由3a≤9,得a≤2,即p:a≤2.
由△=9(3-a)2-4×9≤0,解得1≤a≤5,即q:1≤a≤5.
∵“p∧q”为真命题,
∴$\left\{\begin{array}{l}{a≤2}\\{1≤a≤5}\end{array}\right.$,
解得1≤a≤2.
(2)又t:a<m或$a>m+\frac{1}{2}$,从而$?t:m≤a≤m+\frac{1}{2}$.
∵r是?t的必要不充分条件,即?t是r的充分不必要条件,
∴$\left\{\begin{array}{l}m≥1\\ m+\frac{1}{2}≤2\end{array}\right.$,
解得$1≤m≤\frac{3}{2}$,
∵m∈N*,
∴m=1
点评 本题以命题的真假判断与应用为载体,考查了充要条件,函数的极值,指数不等式的解法,二次不等式的解法,复合命题,难度中档.

练习册系列答案
相关题目
6.在△ABC中,A:B:C=1:2:3,则a:b:c=( )
| A. | 1:2:3 | B. | sin1:sin2:sin3 | C. | 1:$\sqrt{3}$:2 | D. | 1:2:$\sqrt{3}$ |
10.如表是某厂1-4月份用水量(单位:百吨)的一组数据:
由散点可知,用水量y与月份x之间由较好的线性相关关系,其线性回归方程是$\stackrel{∧}{y}$=0.7x+a,则a等于5.25.
| 月份x | 1 | 2 | 3 | 4 |
| 用水量 | 4.5 | 4 | 3 | 2.5 |
20.曲线y=x2+1与两坐标轴及x=1所围成的图形的面积S为( )
| A. | $\frac{1}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
7.已知正项数列{an}中,a1=1,a2=2,2an2=an-12+an+22(n≥2),bn=$\frac{1}{{a}_{n}+{a}_{n+1}}$记数列{bn}的前n项和为Sn,则S33的值是( )
| A. | $\sqrt{99}$ | B. | $\sqrt{33}$ | C. | 4$\sqrt{2}$ | D. | 3 |
5.$\int_2^3{(2x+1)dx=}$( )
| A. | 2 | B. | 6 | C. | 10 | D. | 8 |
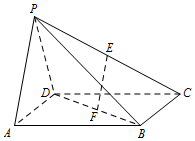 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.