题目内容
8.方程x2+y2-2ax+2=0表示圆心为C(2,0)的圆,则圆的半径r=$\sqrt{2}$.分析 由已知条件求出a=2,由此能求出圆的半径r.
解答 解:∵方程x2+y2-2ax+2=0表示圆心为C(2,0)的圆,
∴a=2,
∴圆的半径r=$\frac{1}{2}\sqrt{16-8}$=$\sqrt{2}$,
故答案为$\sqrt{2}$.
点评 本题考查圆的半径的求法,是基础题.

练习册系列答案
相关题目
19.已知f (x)是可导的函数,且f′(x)<f(x)对于x∈R恒成立,则( )
| A. | f(1)<ef(0),f(2016)>e2016f(0) | B. | f(1)>ef(0),f(2016)>e2016f(0) | ||
| C. | f(1)>ef(0),f(2016)<e2016f(0) | D. | f(1)<ef(0),f(2016)<e2016f(0) |
20.曲线y=x2+1与两坐标轴及x=1所围成的图形的面积S为( )
| A. | $\frac{1}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
17.已知数列{an}满足a1=0,an+1=$\frac{{a}_{n}-\sqrt{3}}{{\sqrt{3}a}_{n}+1}$(n∈N*),则a2010=( )
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | 3 |
18.要得到$y=cos(4x-\frac{π}{3})$的图象,只需将函数y=cos4x图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
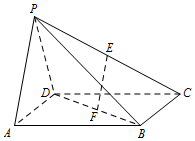 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.