题目内容
12.函数y=x2cosx的导数为( )| A. | y′=x2cosx-2xsin x | B. | y′=2xcos x+x2sin x | ||
| C. | y′=2xcosx-x2sinx | D. | y′=xcosx-x2sin x |
分析 利用两个函数的积的导数法则,求出函数的导函数.
解答 解:y′=(x2)′cosx+x2(cosx)′=2xcosx-x2sinx
故选:C
点评 求函数的导函数,关键是判断出函数的形式,然后据函数的形式选择合适的求导法则.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.曲线y=x2+1与两坐标轴及x=1所围成的图形的面积S为( )
| A. | $\frac{1}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
7.已知正项数列{an}中,a1=1,a2=2,2an2=an-12+an+22(n≥2),bn=$\frac{1}{{a}_{n}+{a}_{n+1}}$记数列{bn}的前n项和为Sn,则S33的值是( )
| A. | $\sqrt{99}$ | B. | $\sqrt{33}$ | C. | 4$\sqrt{2}$ | D. | 3 |
17.已知数列{an}满足a1=0,an+1=$\frac{{a}_{n}-\sqrt{3}}{{\sqrt{3}a}_{n}+1}$(n∈N*),则a2010=( )
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | 3 |
1.下列函数既是增函数,图象又关于原点对称的是( )
| A. | y=x|x| | B. | y=ex | C. | $y=-\frac{1}{x}$ | D. | y=log2x |
2.曲线$y={x^2}+x+\frac{1}{2}$在$({0,\frac{1}{2}})$处的切线方程为( )
| A. | $y=-x+\frac{1}{2}$ | B. | $y=x+\frac{1}{2}$ | C. | $y=-2x+\frac{1}{2}$ | D. | $y=2x+\frac{1}{2}$ |
 如图,D是直角△ABC斜边BC上一点,$AC=\sqrt{2}DC$.
如图,D是直角△ABC斜边BC上一点,$AC=\sqrt{2}DC$.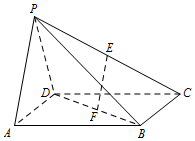 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.