题目内容
13.已知复数z=1+i,则 $\frac{{{z^2}-2z}}{1-z}$=( )| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
分析 把复数z=1+i代入$\frac{{{z^2}-2z}}{1-z}$,再由复数代数形式的乘除运算化简得答案.
解答 解:由z=1+i,
得 $\frac{{{z^2}-2z}}{1-z}$=$\frac{(1+i)^{2}-2(1+i)}{1-(1+i)}$=$\frac{2}{i}=-2i$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列函数既是增函数,图象又关于原点对称的是( )
| A. | y=x|x| | B. | y=ex | C. | $y=-\frac{1}{x}$ | D. | y=log2x |
18.要得到$y=cos(4x-\frac{π}{3})$的图象,只需将函数y=cos4x图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
5.$\int_2^3{(2x+1)dx=}$( )
| A. | 2 | B. | 6 | C. | 10 | D. | 8 |
2.曲线$y={x^2}+x+\frac{1}{2}$在$({0,\frac{1}{2}})$处的切线方程为( )
| A. | $y=-x+\frac{1}{2}$ | B. | $y=x+\frac{1}{2}$ | C. | $y=-2x+\frac{1}{2}$ | D. | $y=2x+\frac{1}{2}$ |
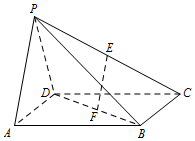 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.