题目内容
19.在△ABC中,内角A,B,C的对边分别为a,b,c,向量$m=(\frac{1}{2}cosA,\frac{1}{2}cosC)$,n=(c,a),且m∥n,则△ABC为等腰或直角三角形.分析 根据向量的共线定理和二倍角公式正弦定理即可求出
解答 解:向量$m=(\frac{1}{2}cosA,\frac{1}{2}cosC)$,n=(c,a),且m∥n,
∴$\frac{1}{2}$acosA=$\frac{1}{2}$ccosC,
由正弦定理可得sinAcosA=sinCcosC,
即sin2A=sin2C,
∴2A+2C=180或2A=2C,
即A+C=90或A=C,
∴△ABC为等腰三角形或直角三角形,
故答案为:等腰或直角
点评 本题考查了向量的共线定理和二倍角公式正弦定理,属于基础题

练习册系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{sin\frac{π}{2}x(0≤x≤2)}\\{lo{g}_{2017}(x-1)(x>2)}\end{array}\right.$,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
| A. | (4,2018) | B. | (4,2020) | C. | (3,2020) | D. | (2,2020) |
14.已知圆O的半径为定长r,点A是平面内一定点(不与O重合),P是圆O上任意一点,线段AP的垂直平分线l和直线OP相交于点Q,当点P在圆上运动时,点Q的轨迹可能是下列几种:①椭圆,②双曲线,③抛物线,④直线,⑤点( )
| A. | ①②⑤ | B. | ①②③ | C. | ①④⑤ | D. | ②③④ |
4.若二次函数f(x)=m2x2+nx+2的图象与x轴有交点,则双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=1$(m>0,n>0)离心率e的取值范围为( )
| A. | (1,3] | B. | [3,+∞) | C. | $(1,\frac{{3\sqrt{2}}}{4}]$ | D. | $[\frac{{3\sqrt{2}}}{4},+∞)$ |
9.若实数a,b,c满足2a=$\frac{1}{a}$,log2b=$\frac{1}{b}$,lnc=$\frac{1}{c}$,则( )
| A. | a<c<b | B. | a<b<c | C. | b<c<a | D. | c<b<a |
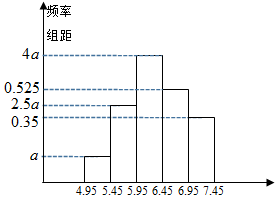 质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下:
质检部门抽查某批次产品的质量(单位:克),随机检查了其中80件产品,根据样本数据描绘的频率分布直方图如下: